Краткие теоретические сведения и методические советы по выполнению курсовой работы, страница 10

Общее решение относительно напряжения имеет вид

2.  Найдём А₁ и А_2. из схемы замещения (рис.2.8) при t®0, когда ω®¥.

Учитывая, нулевые начальные условия и законы коммутации для емкости и индуктивности или условие, когда ω®¥, получим систему

1)   i₂(0) = A₁+ A₂ = 0                           (1)

2)  U₂(0) = Lp₁A₁ + Lp₂A₂ = E             (2)    

(1)  A₁ = -A₂

A₁ = E/L(p₁-p₂),    A₂ =  -  E/L(p₁-p₂)

3.  Найдем p₁,p₂  - корни характеристического уравнения:     .

6. Дальше проводится анализ корней характеристического уравнения и записывается окончательное решение - .

а) если α > w₀, корни – действительные:_. p_1, p₂ < 0, то решение состоит из двух экспонент (рис.2.9). Такое решение называется апериодическим. б) если α < w₀ , корни – комплексные: p₁ = - α + jβ; p₂ = - α - jβ;

В этом случае решение будет представлять собой затухающую гармоническую функцию. Такое решение называется колебательным.

Найдем границу между этими двумя случаями:

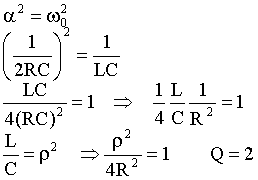
При  Q < 2 – решение имеет апериодический характер

При  Q > 2 - решение имеет колебательный характер.

Пример 2.3. Рассчитать переходную характеристику последовательного колебательного контура (рис.2.10). U₁(t) = E 1(t)

1. Составим дифференциальное уравнение и приведем его к стандартному виду. Уравнение будем составлять, относительно U_C = U₂ , используя 2-ой закон Кирхгофа U_R + U_C + U_L = U₁ и законы Ома для элементов контура, как показано ниже:

. 

2. Общее решение относительно напряжения U₂ имеет вид:

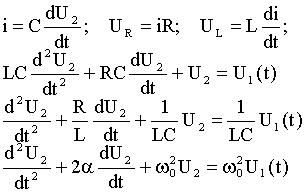
3. Найдем U₂(∞) из схемы замещения (рис.2.11) при t®¥, когда ω=0. Получим U₂(∞) = E .

4.Найдём А₁ и А_2. используя схему замещения (рис.2.12) при t®0, когда ω®¥.

Учитывая, нулевые начальные условия и законы коммутации для емкости и индуктивности, или условие когда ω®¥, получим систему для нахождения A₁,A₂:

при  t = 0,  U₂(0) = A₁ + A₂ + E = 0;  (1)
.

5. Найдем p₁,p₂  - корни характеристического уравнения:

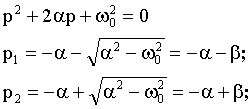
6.Анализ корней и запись окончательного решения.

а) Если α > w₀, то p₁ = - α – β, p₂ = - α + β; корни действительные отрицательные.

   Если  α >> β , то затухание экспоненты преобладает над всеми остальными функциями, т.е. βt→0  → sh0 = 0, ch0 = 1 и общее решение запишется так: б)  Если α < w₀, то  p₁ = - α + jβ, p₂ = - α - jβ; корни комплексные.

 

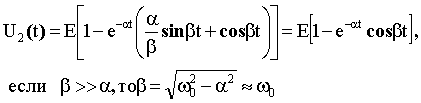
Определим время установления переходного процесса на уровне 0,1:

.  t_уст = 0,7QT , гдеT – период колебательного процесса. Отсюда следует, что Q – добротность, примерно определяется числом периодов, за которое амплитуда колебаний переходной характеристики уменьшается в 10 раз.

Пример 2.4. Для схемы приведенной на рис.2.14а, найти переходную характеристику-.. С1=С2=0.1мкФ, R1=1кОм, R2=10кОм.

Порядок решения:

1. Составим дифференциальное уравнение и приведем его к стандартному виду.

За переменную в дифференциальном уравнении принимаем напряжение снимаемое с конденсатора С₂ оно есть выходное напряжение (отклик) и переменная, характеризующая энергетическое состояние цепи. Выходное напряжение определяется выражением:

,                                          (2.19)

где -ток второго контура. Пользуясь методом контурных токов, составим уравнения для 1 и 2 контуров и установим связь между мгновенными значениями отклика u₂ и воздействия u₁.

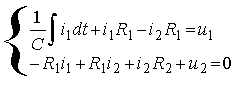,                                       где i₁,  i₂- контурные токи 1-го; 2-го контуров.

Разрешим второе уравнение относительно i₁ и, учитывая, что , получим

.

Подставим i₁ в первое уравнение, получим

.

Сократим однородные члены и путем дифференцирования по времени всех членов уравнения получим дифференциальное уравнение вида:

.                   (4.20)

2. Запишем общее решение дифференциального уравнения второго порядка. Общее решение уравнения (4.20) известно, оно имеет вид: