Пример 1.6. Для цепи (рис.1.14), используя метод контурных токов, вывести выражения для комплексной функции коэффициента передачи напряжений Ku(jw) (его АЧХ - Ku(w) и ФЧХ - jk(w)) и построить графики АЧХ и ФЧХ.
Решение. Топологический анализ показывает:
число узлов nу=2, число ветвей nв=3. Отсюда число
независимых контуров Nв=nу-nв+1=3-2+1=2.
Выбираем направление обхода контуров, как правило, по часовой стрелке. Вводим
обозначения и направления контурных токов ![]() и
и ![]() , как показано на рис.
1.14.
, как показано на рис.
1.14.
Для нахождения ![]() используя МКА необходимо
найти ток
используя МКА необходимо
найти ток ![]() (
(![]() =R3
=R3![]() ). Система уравнений,
составленная по методу контурных токов, имеет вид:
). Система уравнений,
составленная по методу контурных токов, имеет вид:
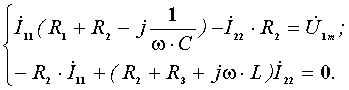
Решая систему по методу
Крамера относительно тока ![]() ,
получаем:
,
получаем:
![]() .
.
Отсюда выражение для комплексного коэффициента передачи напряжения имеет вид:
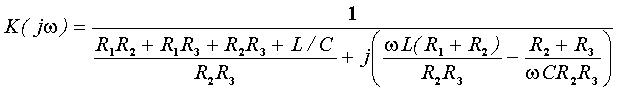 .
.
АЧХ и ФЧХ соответственно равны:
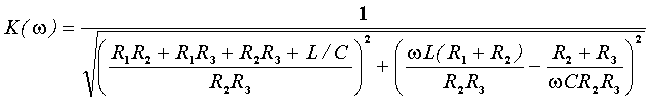 ;
;
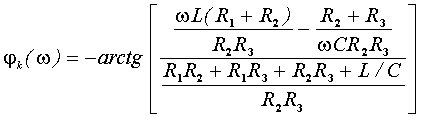 .
.
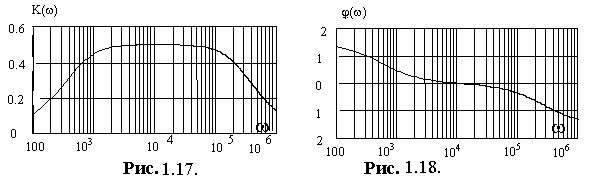 |
Результаты расчета АЧХ и ФЧХ представлены на графиках (рис.1.17 и 1.18). При этом значения частоты взяты в логарифмическом масштабе, т.е. lgw.
Пример 1.7. Решить пример 1.6 методом узловых потенциалов.
Решение. Схема содержит три узла (nу=3). Пронумеруем узлы и введем их обозначения (рис.1.14). Для нахождения U2m необходимо определить j2=U2m. Система уравнений, для нахождения j2, составленная по методу узловых потенциалов, имеет вид:
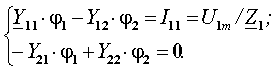
где ![]() ,
,![]() .
.
Решая эту систему относительно j 2 по методу Крамера, получим:
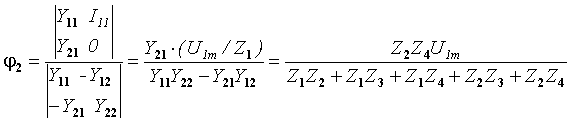 .
.
Отсюда, после подстановок, получим выражение для комплексного коэффициента передачи напряжения:
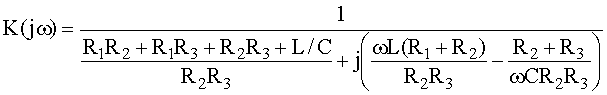 .
.
АЧХ и ФЧХ соответственно равны:
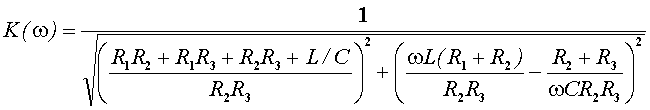 ,
,
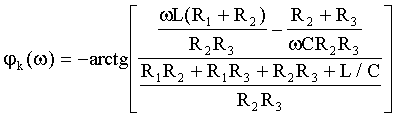 .
.
Сопоставляя результаты расчета в данном примере с результатами предыдущего примера, видим их полное совпадение. Это подтверждает правильность наших расчетов.
Раздел 2
Переходные характеристики электрических цепей
Переходной характеристикой цепи h(t) называют отношение отклика цепи y(t) ( например, выходное напряжение Uy(t) ) к величине X ступенчатого воздействия x(t)=X·1(t) ( например входного напряжения U(t)=Uo·1(t) ) при нулевых начальных условиях (рис.2.1) т.е.
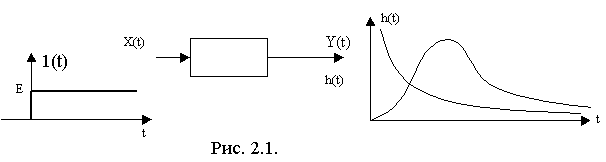 |
Существует ряд аналитических методов расчета переходных характеристик: классический, операторный, спектральный и временной.
рассмотрим классический метод. Классический метод расчета П.Х. сводится к составлению и решению дифференциального уравнения устанавливающего связь между входным и выходным сигналом. Согласно этому методу необходимо:
2.1. Составить дифференциальное уравнение, устанавливающее связь между откликом и воздействием.
2.1.1. Для этого, на основе законов Кирхгофа, или другими приемами решения задач для разветвленных цепей (например, методами контурных токов или узловых потенциалов), составляют уравнения для рассматриваемой цепи относительно мгновенных значений токов, напряжений или зарядов: i, u или q.
При их составлении используются следующие соотношения:
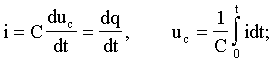 (2.2)
(2.2)
![]()
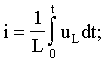 (2.3)
(2.3)
![]()
![]() (2.4)
(2.4)
![]()
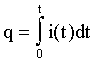 , (2.5)
, (2.5)
где uR, uL, uC - мгновенное значение напряжения на соответствующих элементах цепи.
Составленные уравнения образуют систему интегро-дифференциальных уравнений. За переменные в этих уравнениях обычно принимают переменные состояния - величины, отражающие энергетическое состояние в цепи. Такими величинами являются: iL- токи через индуктивности, UC - напряжения на емкостях. Систему уравнений, составленную для переменных состояния, называют системой уравнений состояния цепи.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.