Краткие теоретические сведения и методические советы по выполнению курсовой работы, страница 6

·  преобразуем исходную схему к виду показанному на рис.1.7, заменив источник эдс на источник тока;

·  потенциал узла 0 примем равным нулю, j₀=0;

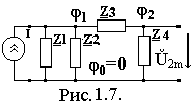·  тогда Ů_2m=j₂ - j₀= j_2.

Составив уравнения по методу узловых потенциалов, получим систему второго порядка и решим ее, относительно j₂, по методу Крамера:

Y₁₁j₁+ Y₁₂j₂=I₁₁

Y₂₁j₁+ Y₂₂j₂=I₂₂, где: Y_{11 –} собственная проводимость первого узла, Y₁₁=(1/Z₁)+(1/Z₂)+(1/Z₃);

Y₁₂ и Y₁₂ – межузловая проводимость Y₁₂= Y₂₁= - 1/Z₃; =-1/Z₃;

Y₂₂ - собственная проводимость первого узла Y₂₂=(1/Z₃) +(1/Z₄);

j_1, j₂ – потенциалы первого и второго узлов;

I_11, I₁₁ – токи источников токов сходящихся в первом и втором узлах.

Отсюда следует, что

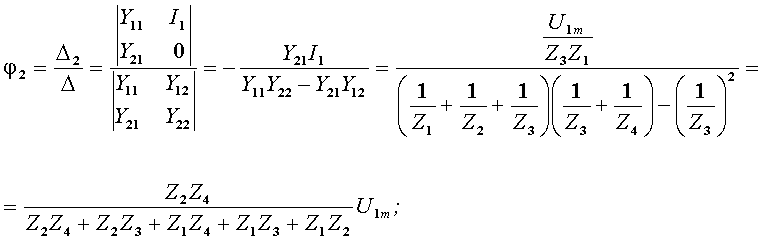K_u(jw)=Ů_2m/Ů_1m =Z₂Z₄/(Z₂Z₄+Z₂Z₃+Z₁Z₂+Z₁Z₃+Z₁Z₄).

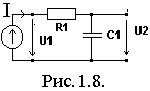Пример 1.3. Для цепи изображенной на рис.1.8 рассчитать:

1.  zвх(jw), z(w), j_z(w).

2.  K_U(jw), K(w), j_K(w).

От исходной цепи переходим к ее комплексной схеме замещения. Она соответствует схеме на рис.1.4.

Используя, определение z_вх(jw) и законы Ома и Кирхгофа получим его выражение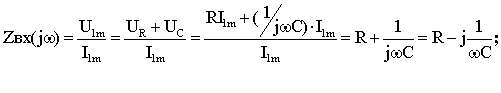

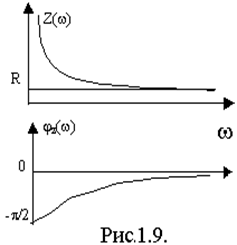
Определим АЧХ и ФЧХ для z_вх(jw) и построим их графики (рис.9), подсчитав значения при w=0, w=¥.

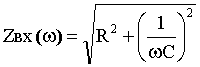;   Zвх(0) = ¥. Zвх(¥) = R.

j_z(w)= -arctg ,   j_z(0)=-p/2, j_z(¥)=0.

Используя, определение K_U(jw) получим его выражение K_u(jw)====.

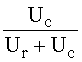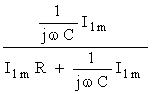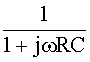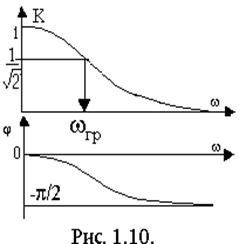
Определим АЧХ и ФЧХ для Ku (jw) и построим их графики (рис.1.10), подсчитав значения при w=0, w=¥.

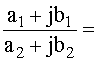
Вспомним, что z== 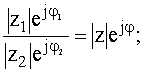где:    тогда,

        Ku(0)=1;      Ku(¥)=0.

Отсюда следует: φ_к(¥)= π/2, φ_к(0)= 0.

Такая цепь пропускает сигналы низких частот (Ku(0)=1) и подавляет сигналы высоких частот (Ku(¥)=0) и называется фильтром низких частот (ФНЧ).

Граничная частота определяется из выражения . Рассчитаем ее для нашего примера:

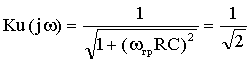, w_грRC=1 Þ .

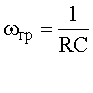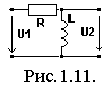
Пример 1.4. Условия прежние. Схема приведена на рис. 1.11.

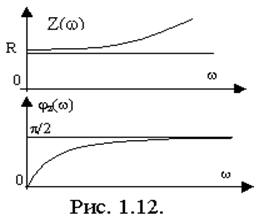
Найдем комплексную функцию входного сопротивления, а также ее АЧХ и ФЧХ и построим графики (рис.1.12).

 От исходной цепи переходим к ее комплексной схеме замещения (рис.1.4). Далее, по аналогии с предыдущем, найдем интересующие нас частотные зависимости:

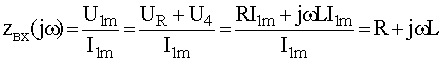; , z(0)=R; z(¥)=¥.

,,j_z(0)=0 ,j_z(¥)=p/2.

Получим выражения для K_U(jw), K_U(w), j_k(ω).

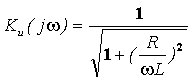,       K_u(0)=0, K_u(¥)=1.

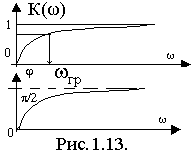
Графики зависимостей K_U(w), j_k(ω) приведены на рис.1.13.

 

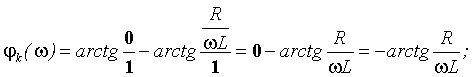
j_k(0)=-p/2;    j_k(¥)=0.

Эта цепь, пропускающая сигналы высоких частот и подавляющая сигналы низких частот называется фильтром высоких частот (ФВЧ).

Определим граничную частоту. По определению . Отсюда:

.

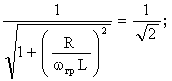
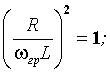
Пример 1.5. Для цепи (рис.1.14) определить комплексную функцию входного сопротивления Z_вх(jw), ее АЧХ  - Z_вх(w) и ФЧХ  -  j₂(w).

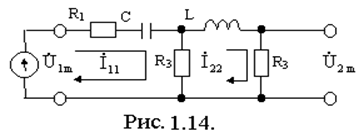Дано: R₁=1кОм R₂=2кОм;          R₃=2кОм; C=1мкФ; L=10^-2Гн.

Решение. Комплексную функцию входного сопротивления находим методом эквивалентных преобразований, перейдя к комплексной схеме замещения (рис.1.5).

На первом этапе преобразуем участок цепи, содержащий последовательное соединение элементов L и R₃. Получим выражение для их комплексного сопротивления Z₃₄=jwL+R₃.

На втором этапе преобразуем участок цепи, состоящий из параллельно соединенных элементов R₂ и Z₃₄. Получим .

На третьем, заключительном, этапе преобразуем участок цепи, содержащий последовательное соединение ветви Z₁, состоящей из последовательного соединения R₁ и C и участка цепи с сопротивлением Z₂₃₄. Получим

.

Запишем полученное выражение в алгебраической форме:

.

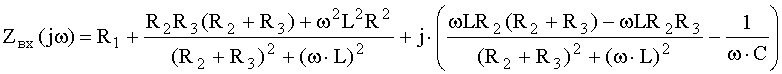Отсюда выражения для АЧХ и ФЧХ имеют вид:

    .

Качественный анализ схемы показывает, что при w=0, т.к. X_с=¥ - входное сопротивление - равно бесконечности, а при w®¥, т.к. X_C=0, X_L=¥, входное сопротивление равно R₁+R₂. Это совпадает с расчетом по полученным выражениям, что подтверждает их правильность.

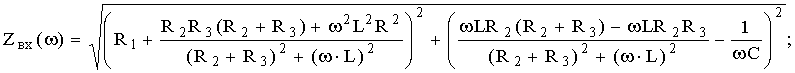
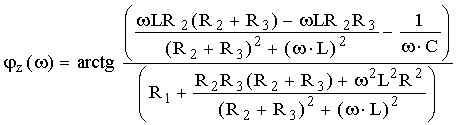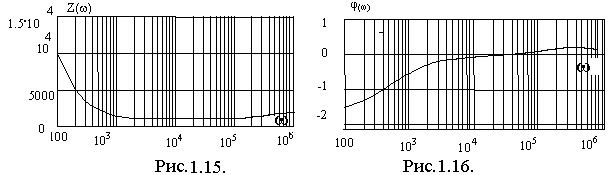Результаты расчета АЧХ и ФЧХ представлены на графиках (рис.1.15 и 1.16). При этом значение частоты взято в логарифмическом масштабе т.е. lg w.