![]() . (4.21)
. (4.21)
3. Найдем вынужденную составляющую общего решения u2(∞) из схемы замещения исходной цепи (рис.2.14б), составленной при t®¥ (w=0).
Анализ цепи показывает, что вынужденная составляющая переходной характеристики, равна
u2(∞) =0.
Отсюда следует, что искомая функция примет вид
![]() . (4.22)
. (4.22)
4. Найдем А1 и А2 исходя из начальных условий. Их находят из начальных условий (при t=0) для искомой функции и ее производных.
Из выражения (4.22) для общего решения следует, что искомая функция при t = 0 равна
u2(t=0)=A1+A2
а производная от искомой функции при t = 0 равна
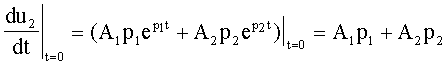 .
.
Учтем, что ![]() , где i2(t=0) ток
второго контура при t=0.
, где i2(t=0) ток
второго контура при t=0.
Определим u2(t=0) и i2(t=0) из анализа схемы при нулевых начальных условиях с учетом законов коммутации. Поскольку напряжение на конденсаторе мгновенно измениться не может, то uc(+0)=uc(-0)=0 , где uc(+0) - напряжение на конденсаторе после подачи скачка напряжения. uc(-0) -напряжение на конденсаторе до подачи скачка напряжения. Последнее, при нулевых начальных условиях, равно нулю, а конденсаторы С1 и С2 на схеме (схема t = 0) представляют собой участки цепи с нулевым сопротивлением. Следовательно, схема замещения исходной цепи при t® 0 (w=¥) имеет вид приведенный на рис.2.14в.
Из анализа этой схемы
замещения следует, что u2(t=0) =0 и i2(t=0) =Е/R2. Отсюда уравнения
для нахождения постоянных интегрирования А1 и А2
принимают вид: ![]()
Из решения этой системы следует:
![]()
Запишем общее решение неоднородного дифференциального уравнения
![]()
5.Найдем корни характеристического уравнения р1=a+b; р2=a-b, где
![]() ;
; 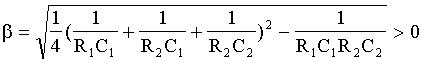
Очевидно, что ![]() , а потому корни вещественны и различны, причем p2<p1<0.
, а потому корни вещественны и различны, причем p2<p1<0.
6. Запишем окончательное решение и проведем анализ ПХ
![]() .
.
![]() Качественный
анализ ПХ показывает, что она состоит из двух экспонент: “быстрой”, с
постоянной времени t2= -1/p2,
и “медленной”, с постоянной времени t1=
-1/p1 (
Качественный
анализ ПХ показывает, что она состоит из двух экспонент: “быстрой”, с
постоянной времени t2= -1/p2,
и “медленной”, с постоянной времени t1=
-1/p1 (![]() ), амплитуды
которых одинаковы по величине, но противоположны по знаку (А1= -А2).
Графики составляющих ПХ и самой ПХ приведены на рис.2.15. Очевидно, что время
нарастания ПХ, т.е. область малых времен будет определяться t2, а время установления ПХ, область больших времен,
постоянной времени t1.
), амплитуды
которых одинаковы по величине, но противоположны по знаку (А1= -А2).
Графики составляющих ПХ и самой ПХ приведены на рис.2.15. Очевидно, что время
нарастания ПХ, т.е. область малых времен будет определяться t2, а время установления ПХ, область больших времен,
постоянной времени t1.
7. Расчет и построение переходной характеристики с помощью ЭВМ
Для определения временного интервала и шага, с которым будем производить расчет графика ПХ, необходимо проанализировать характер функций, составляющих переходную характеристику.
В рассматриваемом примере
ПХ представляется суммой двух экспонент с постоянными временами ![]() и
и ![]() .
.
Если величины ![]() и
и ![]() одного порядка, то за временной
интервал 0-Т1 принимается
одного порядка, то за временной
интервал 0-Т1 принимается ![]() . Шаг изменения времени определим из соотношения
. Шаг изменения времени определим из соотношения ![]() , где n - число точек ПХ (Примем n=20).
, где n - число точек ПХ (Примем n=20).
Если величины ![]() и
и ![]() сильно отличаются (
сильно отличаются (![]() >>
>>![]() ), то расчет ПХ необходимо вести для двух интервалов:
), то расчет ПХ необходимо вести для двух интервалов:
а) для области малых времен примем ![]() с шагом
с шагом ![]() (n=10);
(n=10);
б) для области больших времен примем ![]() с шагом
с шагом ![]() (n=10).
(n=10).
В рассматриваемом примере ![]() =0.001,
=0.001,
![]() =9.01·10-3 ,
=9.01·10-3 , ![]() >>
>>![]() , а
примерный вид ПХ приведен на рис.2.15.
, а
примерный вид ПХ приведен на рис.2.15.
В ряде
случаев ПХ может иметь вид затухающей по экспоненте гармонической функции, вида![]() . В
этом случае за временной интервал принимать T2=(4¸5)/a. За шаг измерения принять величину
. В
этом случае за временной интервал принимать T2=(4¸5)/a. За шаг измерения принять величину ![]() , где
T - период гармонических колебаний Т=2p/b..
, где
T - период гармонических колебаний Т=2p/b..
8. Пример расчета переходных характеристик электрических цепей с помощью пакета математических программ Mathcad.
8.1.Вычислить корни характеристического уравнения р1, р2 и постоянные времени τ1, τ2.
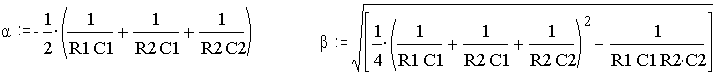
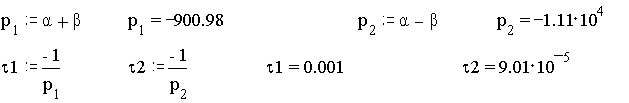
8.2. Вычислить коэффициенты А1 и А2
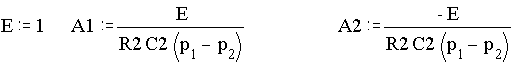
Определим шаг по времени, примем число отсчетов
![]() Т2=5 10-3
Т2=5 10-3
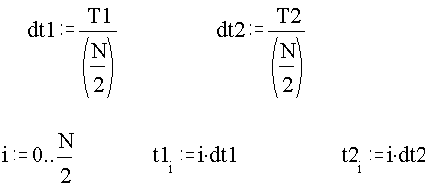
8.3.Введите выражение для переходной характеристики h(t), К=1000,
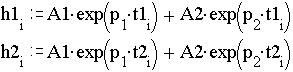
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.