Подбор электродвигателя. Расчет цилиндрической зубчатой передачи, страница 4

2.8.2 Определение коэффициента смещения

;                                                   (35)

Подставляя численное значение, получаем:

.

Для колеса внешнего зацепления , то есть .

2.8.3 Определение  числа зубьев колеса

;                                                       (36)

2.9 Определение фактического передаточного отношения

;                                                         (37)

Подставляя численные значения, получаем:

2.9.1 Определение допускаемого отклонения передаточных чисел

По условию допускаемое отклонение от заданного передаточного числа не должно выходить за пределы ≤4% /1, с. 13/.

;                                                 (38)

Тогда, имеем

.

Следовательно, отклонение от заданного передаточного числа  составляет 0,19%, что меньше допускаемого отклонения.        

18

2.10 Определение диаметров шестерни и колеса

2.10.1 Определение делительного диаметра шестерни и колеса

2.10.1.1 Определение делительного диаметра шестерни

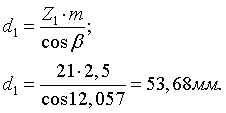                                        (39)

2.10.1.2 Определение делительного диаметра колеса

Для колеса с внешним зацеплением

                                    (40)

2.10.2 Определение диаметра окружности вершин шестерни и колеса

2.10.2.1 Определение диаметра окружности вершин шестерни

                                               (41)

где - коэффициент смещения;

- коэффициент воспринимаемого смещения.

Тогда, получаем:

      

2.10.2.2 Определение диаметра окружности вершин колеса

,                                                      (42)

где - коэффициент смещения;

- коэффициент воспринимаемого смещения.

Тогда, получаем:

19

2.10.3 Определение диаметра окружности впадин шестерни и колеса

2.10.3.1 Определение диаметра окружности впадин шестерни

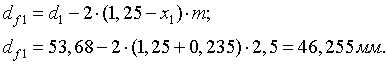                              (43)

2.10.3.2 Определение диаметра окружности впадин колеса

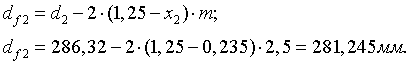                          (44)

2.11 Определение сил в зацеплении

2.11.1 Определение окружной силы в зацеплении

                                                           (45)

2.11.2 Определение радиальной силы в зацеплении

                                                         (46)

где - стандартный угол.

.

2.11.3 Определение осевой силы в зацеплении

                                        (47)

20

2.12 Проверка зубьев колес по напряжениям изгиба

2.12.1 Определение расчетного напряжения изгиба в зубьях колеса

                                 (48)

где - согласно рекомендациям /1, с. 14/;

- коэффициент концентрации нагрузки;

 - коэффициент динамической нагрузки, таблица 2.7 /1, с.15/;

- коэффициент, учитывающий угол наклона зуба /1, с.15/,

;

- коэффициент формы зуба таблица 2.8 /1, с.16/;

- эквивалентная окружная сила /1, с.15/, где  - коэффициент долговечности;

- окружная сила в зацеплении.

.

Таким образом, расчетное напряжение изгиба в зубьях колеса составит:

.

Следовательно, условие (48) выполняется, то есть:

.

2.12.2 Определение расчетного напряжения изгиба в зубьях шестерни

                                                (49)

где - коэффициент формы зуба таблица 2.8 /1, с.16/.

Таким образом, расчетное напряжение изгиба в зубьях шестерни составит:

Что также удовлетворяет условию .

21

2.13 Проверка зубьев колес на статическую прочность при кратковременно действующем пиковом моменте по напряжениям изгиба

2.13.1 Определение статической прочности зубьев шестерни

,                                           (50) где   - пусковой вращающий момент, заданный в расчетно-проекти-ровочной работе;

- максимальное допустимое напряжение изгиба, принима- ется исходя из таблицы 2.2 /1, с.9/.

Подставляя численные значения, получаем:

.

Таким образом, условие (50) выполнимо, то есть:

. 

2.13.2 Определение статической прочности зубьев колеса

,                                           (51)

где   - пусковой вращающий момент, заданный в расчетно-проекти-ровочной работе;

- максимальное допустимое напряжение изгиба, принимается исходя из таблицы 2.2 /1, с.9/.

Подставляя численные значения, получаем: