Подбор электродвигателя. Расчет цилиндрической зубчатой передачи, страница 3

где  - для цилиндрических косозубых колес /1, с.10/.

.

Так как, условие   выполнимо, то есть , то окончательно принимаем для дальнейших расчетов .

2.3.2 Определение допускаемых напряжений изгиба

Исходя из расчетной формулы /1, с. 9/, имеем:

,                                                        (23)

где  – предел выносливости материала, ;

 – коэффициент запаса прочности по напряжениям изгиба.

Исходя из рекомендаций /2, с. 15/, для цементованных и нитроцементован- ных  зубчатых колес - ; для остальных - .

Допускаемые напряжения изгиба определяют отдельно для колеса  и шестерни .

Предел выносливости, для материала колеса исходя из таблицы 2.2  /1, с.9/:

,                                                     (24)

где  – твердость материала колеса.

Тогда

Таким образом, допускаемые напряжения изгиба на колесе составят:

.                                              14                                              

Предел выносливости, для материала шестерни исходя из таблицы 2.2 /1, с.9/:

.                                                     (25)

Таким образом, допускаемые напряжения изгиба на шестерне составят:

.

2.4 Определение межосевого расстояния

Определяем межосевое расстояние исходя из выражения  /1, с.10/:

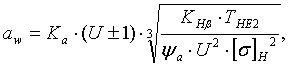                                          (26)

где  знак «-» (в скобках) для передач внутреннего зацепления;

– для косозубых колес /1, с.10/;

– при несимметричном расположении колес относительно опор /1, с.11/;

– коэффициент концентрации нагрузки для прирабатывающих -ся колес (при переменной нагрузке);

 - эквивалентный момент на колесе, где =0,63 – коэффициент долговечности;

 – расчетное допускаемое контактное напряжение.

Таким образом, межосевое расстояние составит:

Следовательно, по таблице 24.1 /2, с.410/ (ГОСТ 6636-69)  из ряда Ra 40 окончательно принимаем межосевое расстояние равное .

2.5 Определение  предварительных основных размеров колеса

2.5.1 Определение делительного диаметра окружности колеса

;                                                      (27)

Подставляя численные значения, получаем:

.                                           15

2.5.2 Определение ширины колеса

;                                                      (28)

Подставляя численные значения, получаем:

.

Окончательно, принимаем ширину колеса по ГОСТ 6636-69 таблица 24.1 /2, с.410/, которая составит .

2.6 Определение модуля передачи

Модуль зацепления определяем по формуле /1, с.12/:

                                                    (29)  

где  - для косозубых колес /1, с. 12/;

 - эквивалентный момент на колесе, где  - коэффициент долговечности;

 - наименьшее допускаемое напряжение изгиба;

Подставляем численные значения, получаем:

.

Полученное расчетное значение модуля округляем  до стандартной величины из ряда чисел /1, с.13/. Таким образом, окончательно принимаем для дальнейших расчетов величину модуля равную .

2.7 Определение суммарного числа зубьев и угол наклона

2.7.1 Определение минимального угла наклона зубьев косозубых колес

;                                                   (30)

Подставляя численные значения, получаем:

.

16

2.7.2 Определение суммарного числа зубьев

;                                                   (31)

Подставляя численные значения, получаем:

Полученное значение суммарного числа зубьев округляют в меньшую сторону до целого числа .

 

2.7.3 Определение действительного значения угла наклона зуба

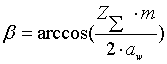;                                                  (32)

Подставляя численные значения, получаем:

.

По рекомендации угол  для косозубых колес лежит в пределах  /1, с.13/.

2.8 Определение числа зубьев шестерни и колеса

2.8.1 Определение числа зубьев шестерни

;                                                 (33)

Подставляя численные значения, получаем

.

Значение  округляем в ближайшую сторону до целого числа. Таким обра –зом, принимаем .

Для косозубых  колес:

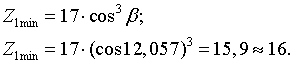                                    (34)

Следовательно, условие (33) выполняется, то есть = .

17