:Штурм-Луивилдің болымсыз операторы, страница 8

        ДӘЛЕЛІ. Егер (2) шекаралық шарттар сызықтық тәуелді болса, онда   деген сан табылып, мына

,  .

теңдіктер орындалады.Онда

.

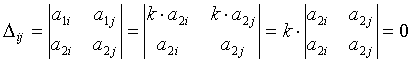Керісінше шекаралық  матрицасының барлық минорлары нөлге тең болсын. Егер шекаралық матрицаның барлық коэффициенттері нөлге тең болса, онда тұжырым айдан анық. Сондықтан қайсібір бағанды нөлден өзгеше болсын деп санаймыз, айқындық үшін . Онда минорлардың нөлге айналу себебінен мынадай  

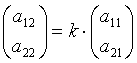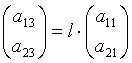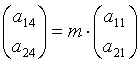,  ,  , мұндағы - әйтеуір бір комплекс сандар.Демек шекаралық  матрицасы мына түрге келеді:

.

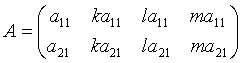Осы матрицаның бірінші жолын -ге көбейтіп, ал екінші жолын  -ге көбейтсек сонан соң алынған нәтижелерді қоссақ нөлдік вектор аламыз, бізге керегі де осы.

АНЫҚТАМА  1.2. Мына,

,                                 (1.5)

шарттарға сай келетін (1) теңдеуінің шешімдерінің фундаменталді системасын ,  арқылы белгілеп, оларды синус және косинус сияқты шешімдер дейміз.

Бірінші теңдеудің жалпы шешімі мынадай                            ,                                                   (1.6)

Болады, мұндағы  әйтеуір бір комплекс сандар.Осы формуланы екінші шекаралық шартқа апарып қойсақ, онда белгісіздері үшін теңдеулер системасын аламыз.

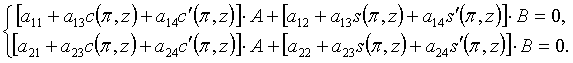                (1.7)

Егер бұл системаның анықтауышы нөлден өзгеше болса, онда , яғни -min бұл мәнінде шекаралық шарттарды тек нөлдік шешім ғана қанағаттандырады, басқаша айтсақ бұл  (1)-(2) шекаралық шарттың меншікті мәні емес. Сонымен егер белгілі бір  үшін (1)-(2) шекаралық есептің нөлден өзгеше шешімі бар болса, онда (7) системаның анықтауышы -min осы мәнінде нөлге айналады, яғни

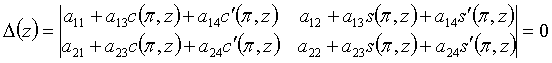.                   (1.8)

Бұл анықтауышты таратып жазсақ мынадай

.                      (1.9)

өрнек аламыз.

Сонымен (1)+(2) шекаралық есептің әрбір меншікті мәні  характеристикалық анықтауышытың нөлі болады, ал бұл функция дәрежесі шектеулі функция болады.

С- комплекс жазықтықтың белгілі бір  нүктесінде  теңдігі орындалсын делік.Бұл сәтте екі түрлі жағдай болуы мүмкін:

1)  Осы нүктеде   анықтауышының барлық элементтері нөлге тең.

2)  Анықтауыштың кемінде бір элементі нөлден өзгеше

Бірінші жағдайда кез-келген  үшін  (6) функция (1)+(2) шекаралық есептің шешімі болады, демек меншікті функциялар жиыны ,  векторларынан туындаған екі салалы кеңістік. Бұл сәтте біз  меншікті мәнін екі еселі дейміз.

Керісінше, егер меншікті мән екі еселі болса, яғни (7) теңдеулер системасының сызықтық тәуелсіз екі шешімі болса, онда (1) теңдеудің кез-келген шешімі меншікті функция болады.

Мысалға, ,  және ,  десек   және деген меншікті функцияларды аламыз. Онда (7) теңдеулер системасынан, характеристикалық анықтауыштың барлық элементтерінің нөлге айналатынын көреміз, яғни

.    (1.10)

Сонымен ,  функцияларының екеуі де (1)+(2) есептің меншікті функциялары болған сәтте  ғана  -меншікті мәні екі еселі болады, яғни тек осы сәтте ғана.

Енді екінші жағдай орын алсын делік, (7)-системаның теңдеулері сызықты тәуелді () болғандықтан олардың біреуін қарастыру жеткілікті, айқындық үшін -ның коэффициенті нөлден өзгеше болсын делік, онда (7) системаның бірінші теңдеуінен   

.

Демек бұл сәтте меншікті функция мынадай

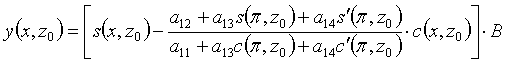,                       (1.11)

болады, мұндағы - кез келген нөлден өзгеше комплекс сан. Осы формуладан, бұл сәтте меншікті функциялар кеңістігі бір салалы екенін байқаймыз.

ЛЕММА 1.2. Егер (2) шекаралық шарттар сызықтық тәуелді болса, онда бүткіл комплекс жазықтық (1)-(2) есептің спектрі болады..

ДӘЛЕЛІ. Бұл сәтте меншікті мәндер мен меншікті функцияларды анықтауға тек бір ғана теңдеу бар болады, ол мынадай

.

Егер белгілі бір  үшін бұл теңдеудің екі коэффициенті де нөлге айналса, онда бұл мән екі еселі меншікті мән болады, басқа жағдайда жайменшікті мән болады.

Мұнан әрі қарай (2) шекаралық шарттар сызықтық тәуелсіз болсын деп жорылық, яғни шекаралық матрицаның кемінде бір миноры нөлден өзгеше делік.

АНЫҚТАМА 1.3. Егер

,                                                    (1.12)

онда (1)+(2)  есепті Штурм-Лиувиллдің болымсыз есебі дейміз.

Штурм-Лиувиллдің болымсыз есебінің спектрәлдік теориясы Биркгофтың, Коддингтонның, Левинсонның, Марчинконың еңбектерінде  кеңінен зерттелген. Сондақтан біз оған тоқталмаймыз.