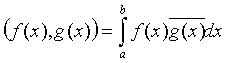:Штурм-Луивилдің болымсыз операторы, страница 5

.

  және  кеңістіктері  жағдайында Гильберт кеңістігі бола алмайтындығына оңай көз жеткізуге болады, өйткені бұл кеңістіктерге енгізілген нормалар (3.1) параллелограмм тепе- теңдігін қанағаттандырады.

Бұл кеңістіктердің барлығы ақырсыз өлшемді, бұл  үшін оңай көрсетіледі: -саналатын векторлар саны сызықты тәуелсіз.

1.3.4. Лебег интегралы ұғымы.

Ескерту 3.1. Осы және төменде келтірілетін интегралдардың барлығы Лебег бойынша интегралданады. Лебег интегралын қалай түсінеміз ?. Жалпы теория бұл сұраққа Лебег өлшемін қолдану арқылы нақты, әрі терең жауап береді. Интегралды қолданушы үшін келесі анықтаманы береміз.

 жиыны нөл өлшеміне ие болады, егер кез келген  саны үшін  болатындай ақырлы немесе саналатын  кесінділер жүйесі табылса. Егер  интервалында өлшемі нөл болатын  функциялар тізбегі үшін f(x) функциясына тең болатын шегі бар болса, онда   интервалында  f(x)  - функциясына барлық жерде дерлік жинақталады дейміз де,  түрінде белгілейміз.

f(x)  - интервалында  Лебег бойынша интегралданады дейміз, егер 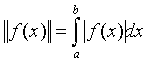 нормасы бойынша фундаментальді үзіліссіз - тізбегі  табылып,  шегі бар болса.  Бұл кезде интеграл ұғымы Риман мағынасында, яғни үзіліссіз функцияның интегралы ретінде түсініледі.Онда f(x) функциясының  аралығындағы Лебег интегралы деп, 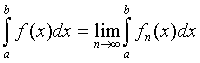  саны аталынады.

Демек, 3.4. мысалында  кеңістігінің элементтері - 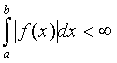 Лебег интегралы ақырлы болатын функциялар, ал  кеңістігі- 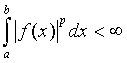 интегралы ақырлы болатын өлшенетін функциялар.

Шегініс 3.1. Көп жағдайда, егер кеңістік   өлшемімен берілсе (мұндағы -саналатын аддитивті, Dom  - -алгебра, х-ке байланысты, егер  болса, онда -өлшемнің толықтығы), онда  кеңістігі деп f комплексмәнді функциялардан құралған кеңістікті айтамыз:

,

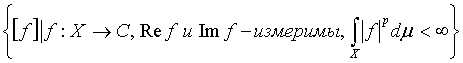мұндағы   -  функциясымен барлық жерде дерлік сәйкес келетін функциялар. Демек, Лебег бойынша интегралдағанда нөл өлшемін ескермейтін болсақ, онда шын мәнінде,  кеңістігінің элементтері ретінде бір-бірінен нөл өлшемі бар жиыны бойынша айырмашылықтары бар, бір-біріне эквивалентті  - функциялар класын қарастыруға болады екен.

Енді егер кеңістік ретінде Z бүтін сандар жиынын алып, ал өлшемді төмендегідей анықтасақ,

, онда  кеңістігі   кеңістігімен сәйкес келеді.

Расында да,  өлшенеді, егер келесі интеграл ақырлы болса

.

Бұл жағдайда

 болады.

Яғни кеңістігі _. –ның дербес жағдайы екен.

Берілген шегініс Лебег интегралы және өлшемі бірдей болатын Лебег кеңістіктері туралы жалпы теорияны бейнелейді. Бірақ, көптеген ұсыныстарда дифференциалдық теңдеулердің шешімін табу есептері үшін Лебегтің қарапайым өлшемі келтіріледі. Бұл өлшемді   3.1. ескертуде келтірілген мағынасында интеграл анықтамасын түсінуге болады.

1.3.5. С.Л.Соболев кеңістігі.

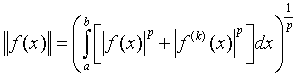Мысал 3.7.  () белгілеуі арқылы  нормасы бойынша  аралығында к рет үзіліссіз дифференциалдау толықтыруы нәтижесінде алынатын функциялардың банах кеңістігін белгілейік.   жағдайында бұл кеңістік скаляр көбейтіндісі :

.

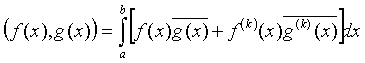болатындай гильберт кеңістігіне айналады.

Шын мәнінде,  барлық жерде Лебег инетгралы қолданылғанымен, толықтыруы нәтижесінде бұл кеңістіктер өте «экстравагантты» функциялар элементіне ие болады.  кеңістігін құрайтын элементтер   аралығында абсолютті үзіліссіз және f'(x) Лебег интегралы, яғни 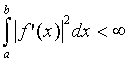  ақырлы болуы қажет. Бұл жердегі берілген кеңістіктің айнымалыларының өлшемі бірден үлкен екенін ескертейік, яғни .

Шегініс 3.2.  Ары қарай, Соболев кеңістігі көбірек қолданылғандықтан абсолютті үзіліссіз функция туралы толығырақ тоқталайық.

       функциясы  аралығында абсолютті үзіліссіз деп аталады, егер  кез келген саны мен кез келген  аралығы  үшін  : : 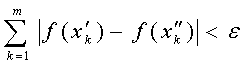теңсіздігі орындалатындай   саны табылса.

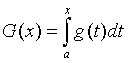Егер  функциясы  аралығында абсолютті үзіліссіз болса, онда   барлық жерде дерлік дифференциалданады және . Кері тұжырым да дұрыс: егер  болса, онда   функциясы  аралығында абсолютті үзіліссіз және осы аралықта   болады.

1.3.6. Ішкі кеңістік. Геометриялықтұрғыдан ең қарапайым кеңістік, ол қасиеттері ақырлы өлшемді евклид кеңістігіне ұқсас Н-гильберт кеңістігі. Дербес жағдайда, x, уН  векторлары ортоганальді деп аталады, егер

(x, у) = 0.

Мысал 3.8.   кеңістігінде скалярлық көбейтіндіге қатысты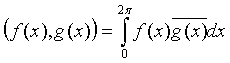  

функциясы ортанормаланған, яғни