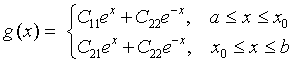:Штурм-Луивилдің болымсыз операторы, страница 7

,                                                   (3.15) мұндағы   - кез келген тұрақты.

(3.15) және (3.12) , (3.14) шарттарын қанағаттандыра отырып,  тұрақтыларын анықтау үшін келесі сызықты теңдеулер жүйесін аламыз:

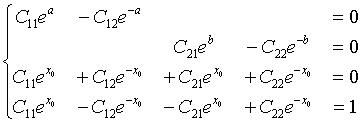                                        (3.16)         

Осы жүйенің анықтауышын есептеп,  табамыз. Сондықтан,   шарты орындалғанда (3.16) системасының бір ғана немесе жалғыз шешімі бар.

 функциясы (3.15) формуласы бойынша жазылғандықтан,  екендігі шығады. Сондықтан  сызықты көпбейнелігі  кеңістігінің ішкі кеңістігін құрайды.

1.3.7. Кеңістіктерді кірістірудің бастапқы түсінігі. Әртүрлі кеңістіктерді қолданғандакеңістіктерді кірістіру түсінігінің маңызы зор.  сызықты нормаланған  сызықты нормаланған кеңістігіне кірістірілді дейміз, бүкіл  жиынында  келесі заңдылық орындалса:, яғни  үшін  теңсіздігі орындалатындай  саны табылса.

Көбінесе бұндай заңдылық ретінде  қолданылады. Бұндай заңдылық кірістіруді орындайды.

(жеңілдету үшін, барлық жерде  аралығы ақырлы саналады ):

·  барлық  кеңістігін , егер ;

·  барлық  кеңістігін  кез келген бүтін ;

·  кеңістіктердің кірістіруі  -ны -ға кез келген  ;

·  Лебег кеңістігінің    егер ;

·  Соболев кеңістігінің кірістіруі   егер ;

·  кірістіру  -ны -ға  егер ;

·  кірістіру  -ны  -ға кез келген , .

Кеңістіктерді кірістіру туралы қосымша қорытындылар үзіліссіз операторды енгізгеннен кейін айтылады.

 1.3.8. Сепарабельді кеңістіктер.  - ақырсыз өлшемді Банах кеңістігі болсын.  тізбегі   кеңістігінің базисі деп аталады, егер  кез келген элементті жинақталатын қатар түрінде жаза алатын болсақ:

.                                                                                        (3.17)

 сандары  элементінің  базисындағы координаталары деп аталады. Демек, кез келген элементті (3.17) түрінде жаза аламыз.  

      ақырсыз элементтер жүйесін называют сызықты тәуелсіз деп атаймыз, егер кез келген  байланысты  ақырлы жүйесі сызықты тәуелсіз болса.

 нормаланған кеңістігі сепарабельді деп аталады, егер осы кеңістікте барлық жерде дерлік тығыз, саналатын жиындар бар болса.Практикада көбінесе қолданылатын кеңістіктер  сепарабельді болып табылады.

Дербес жағдайда, саналатын базистері бар банах кеңістігі-сепарабельді.

Расында да, егер   -   кеңістігінің базисі болса, онда  мүмкін болатын сызықтық комбинациясы (мұндағы ,  және  - рационал сандар)   кеңістігінде барлық жерде дерлік тығыз, саналатын жиынды құрайды.

Теорема 3.2. Кез келген ақырсыз өлшемді сепарабельді  гильберт кеңістігінде саналатын элементтерден тұратын ортогональді базисі бар.

 системасы  гильберт кеңістігінде ортогональді деп аталады, егер   болған жағдайда,  және . Бұл кезде  белгілеуін қолданамыз. Егер қосымша  (яғни ) болса, онда  системасы ортанормаланған деп аталады.

2.  Штурм-Лиувиллдің болымсыз операторы.

2.1. Алғашқы мәліметтер

Мына  кесіндісінде

,                                                                  (1.1)

,              (1.2)

Шекаралық есебін қарастырайық,мұндағы  комплекс мәнді үздіксіз функция, ал    комплекс сандар, -спектрәлді параметр, оның мәндері  -комплекс сандар жиынында өзгерсін деп жорылық.

АНЫҚТАМА  1.1. Осы шекаралық есептің нөлден өзгеше шешімдері бар болған сәттегі  параметрінің мәндерін меншікті мәндер, ал оларға сәйкес шешімдерді  меншікті функциялар дейміз.Осы  (1)-(2) есептің меншікті мәндер жиынын оның спектрі деп атаймыз.

Шекаралық шарттың түріне байланысты спектрдің болмауы, өңдеулі жиын (счетные  множество) болуы немесе бүкіл комплекс жазықтық болуы мүмкін.Мұнан басқа жағдай болуы мүмкін емес, мысалға спектрдің санаулы жиын болуы мүмкін емес.

ЛЕММА 1.1. Егер (2) шекаралық шарттар өзара сызықтық тәуелді болса, онда олардың коэффициенттерінен тұрғызылған мына

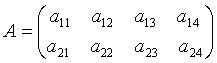                                                        (1.3)

матрицаның барлық минорлары нөлге тең, яғни 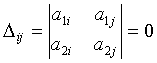                            ,  .                                                               (1.4)

Керісінше егер барлық (4) минорлар нөлге тең болса, онда (2) шекаралық шарттар өзара тәуелді, яғни олардың сызықтық комбинациясы нөлге тең.