:Штурм-Луивилдің болымсыз операторы

 ҚАЗАҚСТАН РЕСПУБЛИКАСЫНЫҢ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТРЛІГІ

ТАРАЗ МЕМЛЕКЕТТІК ПЕДАГОГИКАЛЫҚ ИНСТИТУТЫ

                                                     Математика және МОӘ кафедрасы

Функционалдық анализ пәні бойынша

КУРСТЫҚ ЖҰМЫС

Тақырыбы:Штурм-Луивилдің болымсыз операторы

   Орындаған: М.Қ.

   Тобы: М-14-1

   Курсы: 3

   Жетекшісі: Қ.Ж.

Тараз 2017
                                                              МАЗМҰНЫ

КІРІСПЕ…………………………………………………………………..8

IТарау

1.1.  Түрлендіру операторлары.........................................................15

1.2.  Кесіндідегі Штурм-Лиувиллдің шекаралық есептері.................18

1.3.  Кеңістік туралы түсінік................................................................21

IIТарау

2.      Штурм-Лиувиллдің болымсыз операторы..................................36

2.1.    Алғашқы мәліметтер......................................................................42

2.2.    Штурм-Лиувиллдің болымсыз операторының шекаралық шартын қорытып шығару............................................................................42

Қорытынды.....................................................................................39

Пайдалынған әдебиеттер тізімі........................................................40

                                         КІРІСПЕ

Штурм-Лиувилл операторлары шамамен 1830 жылдан бастап зерттеле бастады десек-те дәл осы күнге дейін өзінің толық шешімін таба қойған жоқ. Көптеген мәселелердің түйіндері тарқатыла қойған жоқ, солардың бірі болымсыз Штурм-Лиувилл операторының спектрәлдік қасиеттері, яғни шекаралық шарттары мына

                                                    (0.1)

теңдіктерді қанағаттандыратын  мынадай

,                                                              (0.2)                                                               

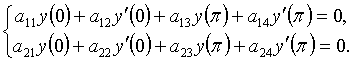                             (0.3)

Штурм-Лиувилл операторлары, мұндағы                         

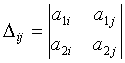,  ,                                           (0.4)         

-Штурм-Лиувилл операторының шекаралық шартының коэффициенті.                Соңғы уақытқа дейін бұл оператордың спектрәлдік қасиеттері туралы ешнәрсе белгісіз еді. Өткен XX-ғасырдың басында пайда болған Биркгофтың теориясына бұл оператор енбей қалған және бұл кездейсоқ жай емес. Қысқаша айтсақ мұндай операторлардың спектрәлдік қасиеттері q(x) коэффициентіне өте тәуелді, ал Биркгоф қарастырған жағдайда бұлай емес еді. Біздің бұл есепке тісіміз бата қоймады, сондықтан тек кейбір дербес жағдайларды қарастырумен шектелдік.

Бұл дипломдық жұмыс екі бөлімнен, кіріспеден қорытындыдан және іс барысында қолданылған әдебиеттер тізімінен тұрады. Бірінші бөлім көмекші қызмет атқарады, барлық негізгі нәтижелер екінші бөлімде келтірілді. Бірінші бөлімде, кейінірек қолданылатын барлық анықтамалар мен негізгі ұғымдар келтірілді.

Екінші бөлімнің бірінші бөлімшесінде Штурм-Лиувиллдің операторлар теориясының негізгі анықтамалары мен қарапайым деректері хабарланды, сонан соң мәселенің мәні айқындалды.

1.1. Түрлендіру операторы

   интервалында Штурм-Лиувиллдің  дифференциалдық теңдеуін қарастырайық:

                                                                 (1.1)

мұндағы- осы интервалдағы үзіліссіз комплексті функция, ал -комплексті  параметр. Кейінірек  функциясын бұл теңдеудің потенциалы немесе  Штурм-Лиувилл операторына сәйкес келетін функция деп атаймыз. Бастапқы берілген (1) теңдеудің шешімін  арқылы белгілейік.

,                                                            (1.2)

(здесь индекс «0» означает, что начальные данные задаются в точке 0, а буква  напоминает, что они такие же, как у функции , с которой совпадает , если ).

ТЕОРЕМА 1.1. (2)  бастапқы берілген (1) теңдеудің шешімі  мына түрде болады:

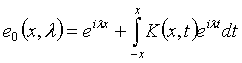,                                                    (1.3)

Мұндағы - үзіліссіз функция, Римана функциясы арқылы өрнектелген теңдеу мынадай

 

, 

мына формуладан                            

.

Интегралдық оператор  мына  формула арқылы анықталған

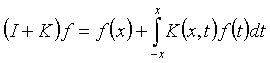, түрлендіру операторы деп атаймыз,  нүктесінде бастапқы шарт сақталынған.Ол мынадай функцияны ( (2) бастапқы берілген қарапайым теңдеу (1) түрінің шешімі ) сол сияқты бастапқы берілген (1) теңдеудің шешіміне көшіреді.  және   функциялары  теңдеуінің шешімінің фундаментальді жүйесін құрастырады.Бастапқы берілген 0-нүктесінде (1)  теңдеудің шешімін    операторы бұл теңдеудің кез келген шешіміне түрлендіреді.Сондықтан бастапқы берілген (1) теңдеуінің шешімі  

,                                                   (1.4)

Мына түрде қарастырсақ:

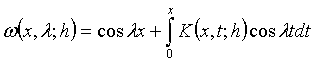,                                    (1.5)

мұндағы                        

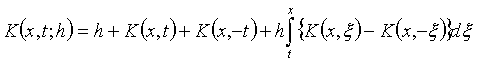.        (1.6)

Бастапқы берілген (1) теңдеудің аналитикалық  шешімі

,                                                  (1.7)