:Штурм-Луивилдің болымсыз операторы, страница 6

.

Есептеу арқылы көз жеткізуге болады.

Н кеңістігінің сызықты, тұйық жиыншасын оның ішкі кеңістігі деп атаймыз. Кез келген  Н үшін кез келген F ішкі кеңістігіне проекциясы, яғни кез келген  f  F үшін  x—x_Ff  болатындай x_F векторы. Осы дәлелге байланысты көптеген геометриялық конструкциялар евклид кеңістігінен Н-қа көшеді, олардың көбісі аналитикалық түрде бейнеленеді. Мысалы, ортогонализациялаудың қарапайым процедурасы  Н кеңістігінде ортанормаланған базис-шексіз   векторларды, кез келген Н , жағдайында   болатындай түрде координаталық жіктелу

                                                                         (3.2)           орындалады, мұндағы .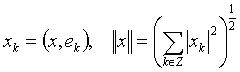

Егер Н кеңістігі ретінде   кеңістігін алып  және  , n=...,—1, 0, 1..., (3.2) формуласына қойсақ, онда ол орташа квадраттық жинақталатын  функциясын Фурье қатарына жіктеуге болады:

.                                                            (3.3)          

Және (3.2) қатынасы  Н пен   кеңістіктерінің ұқсастықтарын көрсетеді, яғниәрбір x(t)Н үшін жалғыз элементі сәйкес келеді және (3.2) формуласы арқылы жазылады.

Мысал 3.9. 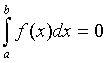 болатын өлшенетін функциялар жиыны   кеңістігінің ішкі кеңістігін құрайды.  3.5 мысалында кірістірілген скалярлық көбейтіндіні ескерсек, біз  үшін   болатындай ішкі кеңістікті сипаттай аламыз. Сонымен қатар, осы ішкі кеңістікті

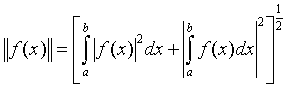
нормасымен анықталған жеке кеңістік ретінде қарастыруға болады. Бұл кеңістік гильберт кеңістігі болады, егер бұл кеңістіктегі скалярлық көбейтіндіні келесі формуламен жазатын болсақ, яғни

. ■

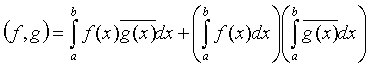Мысал 3.10.

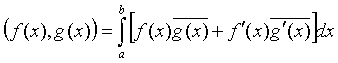                                  (3.4)          скалярлық көбейтіндісімен анықталған гильберттің  Соболев кеңістігінде  сызықты көпбейнелігін қарастырайық, ол қандай да бір  нүктесінде нөл мәнін қабылдасын:

.                                                       (3.5) 

 нүктесі  ішкі кеңістігін құрайтынын көрсетейік, яғни  ішкі кеңістігіне қатысты сызықты тұйық норманы құрайды. Ол үшін  сызықты көпбейнелегі  функциясына ортоганальді болатын  ішкі кеңістікпен сәйкес келетіндей  функциясын табуымыз қажет, яғни

.                                                    (3.6) 

(3.4) формуласында келтірілген скалярлық көбейтіндіні ескере отырып, (3.5) және (3.6) формулаларын салыстыра отырып, кез келген  функциясы үшін келесі қатынас орындалатындығы шығады

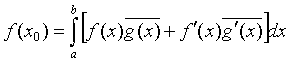.                                       (3.7)          

 функциясын  тегістеу функциялар класында қарастырайық.  функциясы  нүктесінде үзіліссіз дифференциалданбағандықтан, екінші қосындыға бөліктеп интегралдауды қолдану үшін аралықты екіге бөлеміз:  . Онда

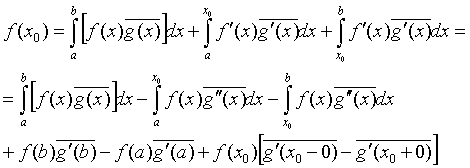                       (3.8) 

Сондықтан,

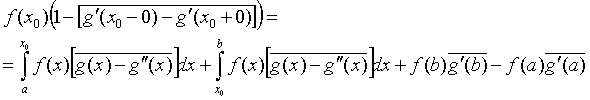.       (3.9)

Егер  функциясы келесі шарттарды қанағаттандырса, онда (3.9) формуласы кез келген  функциясы үшін орындалатынына оңай көз жеткізуге болады.

1)                                                                   (3.10)

2)  және  аралығында  функциясы келесі дифференциалдық теңдеудің шешімі болады.

          .                                                     (3.11)

3) төмендегі шарттар орындалуы қажет:

                                  (3.12)

 болған жағдайда   функциясының бар болатындығын көрсетейік.

Демек, (3.12) «шектік шарттарды»  қанаттандыратын  (3.11) қарапайым дифференциалдық теңдеудің шешімін табу қажет. (3.11) теңдеуі екінші ретті дифференциалдық теңдеу болғанымен, ал шекаралық шарттар үшеу болғанымен бұл есептің шешімі үйлесімді. Өйткені, соңғы шарт шекаралық емес, ішкі шарт болады. (3.11) теңдеуін шешу үшін   нүктесінде бірінші ретті үзілістілік жіберілді, ал шешімнің өзі үзіліссіз, өйтені ол  кеңістігінде жатады. Шешімнің үзіліссіздік шартын келесі түрде жазамыз:

.                                                                   (3.14)

Демек, (3.11) шешімі үшін төрт шекаралық шарттарды алдық:(3.12)+(3.14). Бірақ бұл теңдеуді екінші ретті екі дифференциалдық теңдеу ретінде қарастыруға болады: біріншісі-  аралығында және  екіншісі -  аралығында. Сондықтан, берілген есеп үйлесімді.

Енді бұған есептеу арқылы көз жеткізейік.

(3.11) теңдеуінің әрбір  және  аралықтарында берілген  (3.10) функциялар класындағы жалпы теңдеуінің түрі: