:Штурм-Луивилдің болымсыз операторы, страница 4

Спектральді теорияның ең басты сұрақтарының бірі- меншікті және қосалқы функциялар жүйесінің толықтығын қарастырып отырған кеңістікте зерттеу.  кеңістігіндегі   жүйесінің толықтығы көбінесе  векторына тартылған, яғни  векторының барлық сызықты комбинациясынан құралған сызықты көпбейнеліктің Х жиынында барлық жерде дерлік тығыз екенін дәлелдеу нәтижесінен шығады. Берілген элементтердің қарастырып отырған кеңістікте сызықты қабықшасы тығыз болуы үщін «жиі» немесе «жақын» орналасуы қажеттігі туралы келесі теоремада айтылады.

 Теорема 3.1. (Мюнц).  функциясының сызықты қабықшасы (мұндағы , )   кеңістігінде тығыз болуы үшін  қатарының жинақталуы қажетті және жеткілікті.

Нормаланған кеңістіктердің толықтығын түсіндіру үшін келесі лемманы қарастырайық.

 Лемма 3.1. (тізбектердің жинақталуы туралы). Кез келген  жиыны үшін нормаланған (толық емес болуы мүмкін)  кеңістігінде келесі тұжырымдар эквивалентті:

1)  жинақталады;

2)-тізбегінің кез келген  -тізбекшесі жинақталады;

3)  -тізбегі  фундаментальді және берілген  - тізбекшесі жинақталады;

4)  -тізбегі  фундаментальді және  - жинақталатын тізбекшесі бар;

5)  - қатары жинақталады.

 тізбегінің тізбекшесі деп, ,  ретімен құралған  тізбекті айтамыз, яғни    тізбекшесінің  тізбегінің элементтерінің реті сақталады екен.

1.3.2. Гильберт кеңістігі. Көптеген есептердеерекше дербес жағдай туындайды, егер   сызықтық кеңістігінде евклидтік кеңістігіндегі қарапайым скалярлық көбейтіндінің жалпылауы болатын скалярлық көбейтіндіні енгізсек. Яғни, x, у элементтерінің скалярлық көбейтіндісі деп, (x, у) деп белгіленетін келесі қасиеттерді қанағаттандыратын комплекс санды айтамыз.

·  Барлық кезде (x, x)  0 және  (x, x) = 0, тек қана x = 0 болған жағдайында ;

·  ;

·  , кез келген С.

   саны норманың барлық аксиомаларын қанағаттандырады. Сондықтан, x  элементінің нормасы ретінде  санын аламыз. Бұндай кеңістікті сыртқы Гильберт кеңістігі деп атаймыз. Функционалдық талдауды негіздеу үшін, қарастырып отырған кеңістіктің толық болғандығы маңызды ( кеңістіктің элементтерінің фундаментальді тізбегі осы кеңістіктің элементіне жинақталуы үшін, яғни кез келген x_m, x_nХ үшін n, m →∞ , ||x_n — x_m||  → болса, онда Х жиынының элементі болатындай  шегі табылады).

Толық сызықты нормаланған және толық сыртқы гильберт кеңістігі, сәйкесінше, банах және гильберт кеңістігі деп аталады. Бұл жағдайда, метрикалық кеңістіктің толықтыруы ретінде (рационал саннан нақты санға өтуі) сызықты нормаланған кеңістік банах (гильберт) кеңістігіне келтіреді.

Егер кеңістіктегі норма  скалярлық көбейтіндіден туындаса, онда «параллелограмм тепе-теңдігі орындалады»:

.                                                          (3.1) 

Кәдімгі евклидтік кеңістік гильберт кеңістігінің қарапайым мысалы бола алады. Гильберт кеңістігі ретінде комплексті бағандардың  кеңістігін де алуға болады және онда скалярлық көбейтінді келесі формуламен анықталады:

  для всех .

Бірақ, функционалдық талдауда басты рөлді ақырсыз өлшемді кеңістіктер, яғни сызықты тәуелсіз векторлардың ақырсыз санынан құралған кеңістіктер атқарады.

 1.3.3. Функционалдық кеңістіктердің негізгі мысалдары.

Мысал 3.2.Элементтері -  тұйық интервалында   нормасымен анықталған үзіліссіз комплексмәнді функциялар болатын Банах кеңістігі. Бұл кезде  кеңістігінде норма бойынша жинақталу- математикалық анализ курсынан белгілі бірқалыпты жинақталу болып табылады.

 Мысал 3.3. тұйық интервалында , (мұндағы - к-ші ретті f(x) функциясының туындысы) нормасымен анықталған комплексмәнді үзіліссіз дифференциалданатын функцияларынан құралған  Банах кеңістігі.  - тізбегінің жинақталуы – бұл  тізбектерінің  интервалындағы бірқалыпты жинақталу.

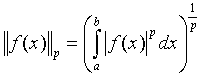Мысал 3.4. интервалында (p  1) функция дәрежесімен анықталған барлық р бойынша қосындыланатын   Банах кеңістігі.  кеңістігіндегі норма бойынша жинақталу деп, ал   - кеңістігіндегі норма бойынша тізбектердің жинақталуын орташа квадраттық жинақталу деп атайды.

Мысал 3.5.(бүтін сандар жиыны) ақырсыз тізбектерінің , ал нормасы 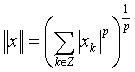бойынша анықталатын  -Банах кеңістігі.

Мысал 3.6.p = 2 жағдайында   және - гильберт кеңістіктері, мысалы,  -да скалярлық көбейтінді