:Штурм-Луивилдің болымсыз операторы, страница 3

                                теңдеуін қанағаттандыратын меншікті және қосарланған функциялар тізбегін қорытып шығарайық.

Бөліктелген шекаралық шарттармен берілген

,                            (2.9)

шекаралық есептерді қарастыра отырып

,  ,  ,  ,  .            (2.9^/)

аламыз. Бұдан   болған жағдайда  шекаралық шарт болымды, ал меншікті жүйе және қосарланған функция толығымен кеңістігінде жатады.

Шындығында,меншікті және қосарланған функциялардың (1),(9) шекаралық шарттары  кеңістігінде базис құрады..

1.3.1. Нормаланған кеңістік. Функцианалдық тандаудағы көбінесе кездесетін жалпы кеңістіктер сызықтық (векторлық) топологиялық  кеңістік, яғни C комплекс сандар  өрісінің (немесе R  нақты сандарының ) сызықтық кеңістік болып табылады. Бұл кеңістік бір мезгілде топологиялық және сызықты операциялар осы кеңістікте үзіліссіз. Дербес, бірақ өте қажетті жағдай,  сызықтық кеңістігінде қасиеттері қарапайым евклидтік кеңістігінің векторлар ұзындығының қасиеттерінің жалпыламасы болатындай векторлар нормасын (ұзындығын) сиғызуға болады. Дәл элементінің нормасы деп,  және  тек қана  болған жағдайда орындалатын  - нақты санын атаймыз.

,        

, егер( ) болса және  - ”үшбұрыш теңсіздігі„ орындалса

 сызықтық кеңістігіндегі екі түрлі  және  нормасын енгізейік.  және  номалары эквивалентті деп аталады, егер кез келген  үшін  теңсіздігі орындалатындай   сандары табылса.Бұдан еуі норма сызықтық кеңістікте эквивалентті  әрқайсысы бір-біріне тәуелді болатыны анық.Бұл жағдайда егер Х сызықтық кеңістігінде екі эквивалентті норма және Х₁ және Х₂ – сәйкесінше нормаланған кеңістіктері берілсе, онда берілген кеңістіктердің бірінде жинақталатын қатар,екінші кеңістікте де сондай шекке жинақталады.Бұл жайт,әр кеңістікте өзімізге жұмыс істеуге ыңғайлы эквивалентті нормалардың бірін таңдауға мүмкіндік береді.

Егер қарастырып отырған Х кеңістігіміз – ақырлы өлшемді болған жағдайда,норманы таңдау кеңістікті өзгертпейді.Анығырақ: Кез келген ақырлы өлшемді сызықтық кеңістікте барлық нормалар эквивалентті.

Мысал 3.1. Евклид кеңістігі.-сызықты жүйесі мүмкін болатын барлық n- өлшемді  векторларынан құралсын.. Егер  - кеңістігінде келесі нормалардың бірін енгізе алсақ, яғни  немесе 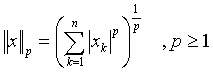   , онда -евклидтік кеңістігі деп аталатын нормаланған кеңістікті аламыз. Нормалардың аксиомалары сөзсіз тексеріледі. Бұл кезде, екінші норма үшін үшбұрыш теңсіздігі ақырлы қосынды үшін Минковский теңсіздігінің қолдану салдары болып табылады. .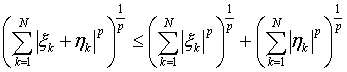

Егер векторлар «координатасы» комплекс сандар болса, онда     немесе    ,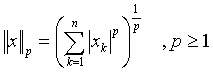

(мүндағы  - -комплекс санның модулі) нормасымен анықталған  векторының комплекс бағанынан құралған сызықтық система нормаланған кеңсітік болып және евклидтік кеңістік тәріздес  деп белгіленеді.

 нүктесі  жиынының шектік нүктесі деп аталады, егер  нүктесінің кез келген маңайында  нүктесінен өзге болатын М жиынының кемінде бір нүктесі жатса. Басқа сөзбен айтқанда,  -   жиынының шектік нүктесі дейміз, егер кез келген  шарында  нүктесі табылса.  нүктесі  жиынының шектік нүктесі болуы үшін , . нүктесіне жинақталатын тізбегінің бар болуы қажетті және жеткілікті.

   , ал   – М жиынының шектік нүктелер жиыны болсын. Онда  жиыны М жиынының тұйықталуы деп аталады. Басқа сөзбен айтқанда,  - бұл құрамында М жиыны бар өте кішкентай тұйық жиын.   болатын М жиыны тұйық деп немесе берілген жиын тұйық деп аталады, егер шектік нүктелерінің бәрі өзінде жатса.

 сызықтық кеңістігіндегі  жиыны сызықты көпбейнелік деп талады, егер кез келген  және  сандары үшін  сызықтық комбинациясы   жиынында жатса.  жиыны  жиынының бір бөлігі болғандықтан, сызықты көпбейнеліктің анықтамасынан  жиыны да сызықтық кеңістік екендігі шығады. Мұндай  жиыны нормасы бойынша  жиынында тұйық болмайтынын ескерту қажет.

 () нормаланған кеңістігінде жататын  сызықты көпбейнелігін  жиынында тығыз дейміз, егер  и  саны үшін  теңсіздігі орындалатындай  элементі табылса. Демек, егер   жиынында тығыз болса, онда  үшін  болатындай  тізбегі табылады.

Жоғарыда айтылған анықтаманы тұйықталумен салыстырсақ, « жиыны  жиынында тығыз», , тұжырымы  сызықты көпбейнеліктің  нормасы бойынша тұйықталуы -пен сәйкес келетінін байқаймыз. Бұл кезде,    кеңістігін  нормасы бойынша   сызықты көпбейнеліктің толықтырушысы деп те атаймыз. Әрбір сызықты нормаланған  кеңістігінің толықтырушысы бар және бұл толықтырушы  -ті өзіне көшіретін изометриялық бейнесіне дейін дәл болатын жалғыз жиын.