Мына түрде беруге болады
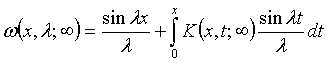 ,
(1.8)
,
(1.8)
мұндағы
![]() .
(1.9)
.
(1.9)
Осы 1.1. теоремасынан мынадай салдар шығады.
САЛДАР 1.1. (4), (7) бастапқы берілгендер үшін (1) теңдеудің шешімін мына түрде жазуға болады
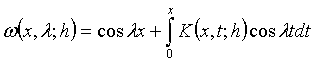 ,
(1.10)
,
(1.10)
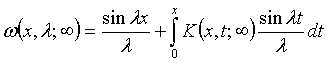 ,
(1.11)
,
(1.11)
мұндағы ![]() функция,
функция, ![]() функциясы (6), (9) формуласындағы (3) операторының
функциясы (6), (9) формуласындағы (3) операторының ![]() ядросы бойынша өрнектеледі.
ядросы бойынша өрнектеледі.
(3), (10), (11) теңдігінің оң жағында
анықталған ![]() ,
, ![]() ,
, ![]() , операторын 0 нүктесіне байланған түрлендіру
операторы деп атаймыз.
, операторын 0 нүктесіне байланған түрлендіру
операторы деп атаймыз.
ЛЕММА 1.1. Егер (2) бастапқы берілгендер
үшін (1) теңдеудің ![]() шешімі барлық
шешімі барлық ![]() мәнінде (3) формуламен
берілсе, онда
мәнінде (3) формуламен
берілсе, онда ![]() ядросы мына теңдеуді
қанағаттандырады
ядросы мына теңдеуді
қанағаттандырады
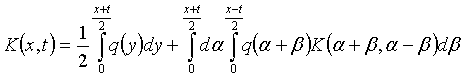 (1.12)
(1.12)
және, керісінше, егер ![]() функциясы
(12) теңдеуін қанағаттандырса, онда (3) формуласы оң жағындағы
барлық
функциясы
(12) теңдеуін қанағаттандырса, онда (3) формуласы оң жағындағы
барлық ![]() мәндерінде үшін (2) бастапқы
берілгендер үшін (1) теңдеудің
мәндерінде үшін (2) бастапқы
берілгендер үшін (1) теңдеудің ![]() шешімі болады.
шешімі болады.
ТЕОРЕМА 1.2. (12) теңдеудің жалғыз ғана шешімі бар. Бұл шешім үзіліссіз және мына теңсіздікті қанағаттандырады
![]() ,
(1.13)
,
(1.13)
мұндағы
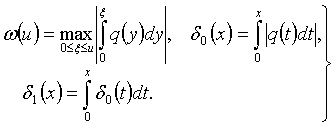 (1.14)
(1.14)
Егер ![]() функциясы
функциясы ![]() үзіліссіз туындысы болса, онда
үзіліссіз туындысы болса, онда![]() ядросының
ядросының ![]() екі жақты алмастыру бойынша
үзіліссіз туындысы бар.
екі жақты алмастыру бойынша
үзіліссіз туындысы бар.
САЛДАР 1.2. ![]() функциясы (3) түрлендіру
операторының ядросы болу үшін
функциясы (3) түрлендіру
операторының ядросы болу үшін ![]() функциясы Гурс есебінің
шешімі болуы қажетті және жеткілікті:
функциясы Гурс есебінің
шешімі болуы қажетті және жеткілікті:
![]() ,
, 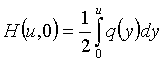 ,
, ![]() . (1.15)
. (1.15)
Егер ![]() функциясы үзіліссіз
дифференциалданса, онда (1.15) есебі былай түрленеді:
функциясы үзіліссіз
дифференциалданса, онда (1.15) есебі былай түрленеді:
![]() ,
, 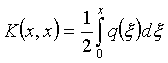 ,
, ![]() . (1.16)
. (1.16)
1.1. Ақырғы интервалдағы Штурма-Лиувиллдің шекаралық есебі
![]() аралығында Штурма-Лиувилл
теңдеунің шекаралық есебін қарастырайық:
аралығында Штурма-Лиувилл
теңдеунің шекаралық есебін қарастырайық:
![]() ,
(2.1)
,
(2.1)
және екі шекаралық шарттармен ![]() :
:
![]() , (2.2)
, (2.2)
мұндағы ![]() - қосатын комплексмәнді
функция,
- қосатын комплексмәнді
функция, ![]() - туындылы комплексті сандар.
- туындылы комплексті сандар.
Параметрмәні ![]() болғанда, мұндай шекаралық
есептердің нөлдік шешімдері болса, онда оны меншікті мән деп атаймыз, ал оған
сәйкес шешім- меншікті функция деп аталады. (1) теңдеуінің фундаментальді жүйесінің
шешімі мына анықталған бастапқы берілгендерді
болғанда, мұндай шекаралық
есептердің нөлдік шешімдері болса, онда оны меншікті мән деп атаймыз, ал оған
сәйкес шешім- меншікті функция деп аталады. (1) теңдеуінің фундаментальді жүйесінің
шешімі мына анықталған бастапқы берілгендерді ![]() ,
, ![]() мынау
мынау ![]() ,
, ![]() арқылы белгілейік ( сонымен
арқылы белгілейік ( сонымен ![]()
![]() алдынғы бөлімшеде
белгіленген ). Сондықтан (1) теңдеуінің
алдынғы бөлімшеде
белгіленген ). Сондықтан (1) теңдеуінің ![]() жалпы шешімі
жалпы шешімі ![]() ,
, ![]() :
: ![]() функциясының сызықты
комбинациясы болса, онда
функциясының сызықты
комбинациясы болса, онда
![]() , (2.3)
, (2.3)
бұдан, (1), (2) шекаралық есептің нөлдік шешімі болады сонда ғана, егер теңдеулер жүйесі
![]() ,
,
![]() ,
,
![]() коэффициенттерінің нөлдік
шешімі болса. Сондықтан меншікті мән қарастырылған есепке квадрат түбірмен оның
характеристикалық функциясы сәйкес келеді.
коэффициенттерінің нөлдік
шешімі болса. Сондықтан меншікті мән қарастырылған есепке квадрат түбірмен оның
характеристикалық функциясы сәйкес келеді.
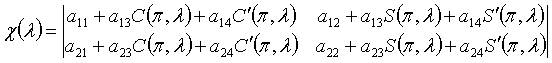 . (2.4)
. (2.4)
Мына анықтауышты ескере отырып
вронскиан ![]() бірге тең болатындығын
көреміз, сол арқылы
бірге тең болатындығын
көреміз, сол арқылы
![]() , (2.4/)
, (2.4/)
Функциясын табамыз. Мұндағы ![]() -анықтауыш, шекаралық
шарттың коэффициенті
-анықтауыш, шекаралық
шарттың коэффициенті ![]() ,
, ![]() матрица бағандарынан
құралған.
матрица бағандарынан
құралған.
 .
.
Бұдан ![]() болғанда, (1)-(2) шекаралық
есептің
болғанда, (1)-(2) шекаралық
есептің ![]() характеристикалық функциясы
мына түрге келеді:
характеристикалық функциясы
мына түрге келеді:
![]() (2.6)
(2.6)
және қарапайым жағдайда, яғни ![]() функцисы нөлден өзгеше
болғанда меншікті жүйенің толықтығы және тек шекаралық шарттарға қоюға болатын
қосарланған функция туралы сұрақ туады. Бұл келесі 3 шарттың орындалу
мүмкіндігін көрсетеді:
функцисы нөлден өзгеше
болғанда меншікті жүйенің толықтығы және тек шекаралық шарттарға қоюға болатын
қосарланған функция туралы сұрақ туады. Бұл келесі 3 шарттың орындалу
мүмкіндігін көрсетеді:
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() . (2.7)
. (2.7)
Шекаралық шарт бұлардың кемінде біреуін қанағаттандырса, онда ол болымды деп аталады.
ТЕОРЕМА 2.1. (1)-(2)
толық болымды шекаралық шарттармен берілген меншікті жүйе және қосарланған
функцияның шекаралық есебін ![]() кеңістігінде қарастырған.
кеңістігінде қарастырған.
Қосарланған функция анықтамасын еске түсірейік.
(4) анықтауышын ![]() элементі арқылы белгілеп, (1)
теңдеуінің шешімін құрастырайық:
элементі арқылы белгілеп, (1)
теңдеуінің шешімін құрастырайық:
![]() .
(2.8)
.
(2.8)
(3) формуласынан тура ![]() -ға тең екендігін көреміз.
-ға тең екендігін көреміз.
![]() ,
,
![]() .
.
(1)-(2) шекаралық есептің ![]() меншікті мәні
меншікті мәні ![]() - еселік деп аталады, егер
- еселік деп аталады, егер ![]()
![]() функциясының
функциясының ![]() еселік түбірі болса.
еселік түбірі болса.
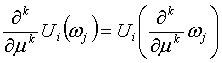 ,
, ![]() , болса, онда функция
, болса, онда функция
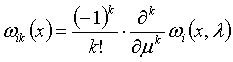 ,
, ![]()
![]() - (2) шекаралық шартын
қанағаттандырады,егер
- (2) шекаралық шартын
қанағаттандырады,егер ![]() болса.
болса. ![]()
![]() функциялары тізбек
құралады, біріншісі нөлден өзгеше
функциялары тізбек
құралады, біріншісі нөлден өзгеше ![]() функциясы меншікті болады,
ал келесілері функцияларға қосарланған. (1) теңдеуін
функциясы меншікті болады,
ал келесілері функцияларға қосарланған. (1) теңдеуін ![]() рет
рет ![]() бойынша дифференциалдай
отырып , (2) шекаралық шартын және
бойынша дифференциалдай
отырып , (2) шекаралық шартын және
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.