Структурный анализ в решениях последовательных данных: Учебное пособие (Многовариантная алгоритмизация и применение сглаживающих фильтров. Теоретические основы структурного анализа), страница 18

                 ,                        (2.3)

где M – символ математического ожидания; R – корреляционная функция;

τ – сдвиг корреляционной функции.

Когда

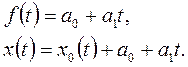                                                                  (2.4)

Выражение для структурной функции запишется следующим образом:

.  (2.5)

Для данного типа нестационарности структурная функция не зависит от времени и, следовательно, процесс с линейным трендом является процессом со стационарными первыми приращениями.

Если же

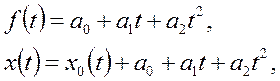                                                        (2.6)

то

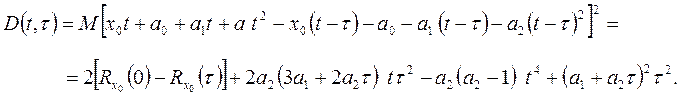    (2.7)

Структурная функция зависит от времени.

При

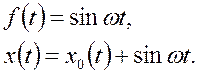                                                                     (2.8)

Тогда

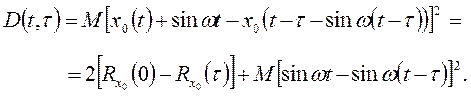                      (2.9)

В этом случае, если период колебания функции f(t) значительно меньше времени наблюдения процесса x(t), то

                                                     (2.10)

и, следовательно, структурная функция не зависит от времени. При сопоставимости периода колебания с продолжительностью наблюдения процесс не обладает свойством стационарности первых приращений.

Таким образом, для рассмотренных случаев можно сделать вывод об инвариантности структурной функции только относительно линейного тренда.

Для стационарного процесса структурная функция просто выражается через корреляционную функцию:

                   .                                            (2.11)

Знание корреляционной функции позволяет определить структурную функцию. Обратное утверждение возможно в том случае, если из физических представлений ясно, что связь между значениями x(l) и x(l+τ) затухает при τ → ∞ и R(τ) = 0. В этом случае

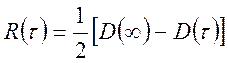                  ,                                           (2.12)

т.е. для стационарных случайных процессов в затухающей на бесконечности корреляционной функции статистические характеристики D(τ) и R(τ) взаимосвязаны и по одной из них всегда можно определить другую. Это свойство используется для определения стационарности случайных процессов.

На рисунке 2.1 приведены структурные функции D(τ), автокорреляционные функции R(τ) и их оценка  по формуле (2.12) для нестационарного по математическому ожиданию широкополосного случайного процесса.

Рисунок 2.1 – АКФ стационарного а) и нестационарного б) по      математическому ожиданию случайных процессов

На рисунке 2.2 приведены нормированные структурные функции для таких реализаций переменных, как расход кокса в подачу, влажность и температура дутья в доменной печи. По виду графиков можно предположить примерно одинаковое строение реализаций влажности и температуры дутья.

Для нестационарного случайного процесса характерно систематическое смещение между фактическим и рассчитанным по формуле (2.12) значениями АКФ. Во втором случае совпадение между фактической и рассчитанной АКФ лучше, систематическое смещение отсутствует. Статистический анализ значимости отличия автокорреляционных функций затруднён вследствие специфических свойств исследуемых процессов, таких как нестационарность, негауссовское распределение, зависимость измерений друг от друга и т.д.      

   Рисунок 2.2 – Структурные функции реализаций влажности дутья (1),

температуры дутья (2) и расхода кокса в подачу (3)

Чтобы обеспечить возможность сравнения структурных функций для различных по физической природе процессов, их целесообразно нормировать. Из-за трудности оценки D(∞) на конечных реализациях переменных будем осуществлять нормировку делением значений структурной функции на дисперсию процесса , т.е.

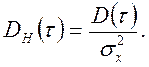                                                                           (2.13)

Расход кокса в подачу имеет отличающуюся структуру и характеризуется значительной нестационарностью по математическому ожиданию.

Некоторые типы нестационарных случайных процессов могут быть представлены в виде соотношения, в котором Δх – стационарная составляющая случайного процесса х; m – число усредняемых данных:

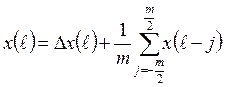,                               (2.14)