В настоящей работе для сжатого описания выборок конечных реализаций сигналов, эквивалентных по особым точкам, используется модель генерирования финитных случайных функций, согласно которой ансамбли реализаций порождаются в результате преобразования некоторых характеристик (эталонных) скалярных или векторных кривых. Эта модель имеет тесные аналоги с механизмом порождения изобретений, принятым в непрерывно-групповой теории распознавания образов, и с параметрическим заданием кривых.
На этапе формирования выборок с желаемыми свойствами координаты особых точек на эталонных кривых задаются приближённо. Для их уточнения или первичного определения, если случайные функции формируются без непосредственного указания эталонов, следуем производить раздельное усреднение абсцисс и ординат соответственных особых точек единичных реализаций выборки.
Для аппроксимации преобразования характерных кривых в фактические усечённые реализации сигналов могут быть использованы уравнения групп Ли или обычные степенные и ортогональные полиномы. Последние более приспособлены для аппроксимации деформаций векторных кривых производственных объектов, так как особые точки единичных реализаций оцениваются с ошибками, предпосылки топологических преобразований выполняются только приближённо, и коэффициенты уравнений приходится отыскивать, например, методом наименьших квадратов. Если объём выборок отрезков сигналов большой (более одного-двух десятков), для дальнейшего свёртывания информации нужно строить вероятностные распределения значений коэффициентов уравнений деформации характерных кривых.
Изменения переменных производственных процессов между поворотными (по тенденции) точками хорошо аппроксимируются линейными от аргумента выражениями с наложением стационарной случайной помехи в виде белой или марковской последовательности. Такой способ описания поведения сигналов между особыми точками позволяет определять для периодических и непрерывных производственных процессов хорошо интерпретируемые усреднённые кривые, которые содержат достаточную информацию о компактных выборках при решении ряда задач изучения и оптимизации объектов.
2.2 Структурный анализ рядов данных с использованием
функционалов отличия
2.2.1 Получение структурных функций
Реализации контролируемых переменных, характеризующие работу технологических и рыночных объектов, представляют собой случайные процессы времени и не всегда обладают стационарными эргодическими свойствами. При их исследовании, наряду с такими интегральными характеристиками как корреляционная функция и спектральная плотность, являющимися способами адекватного описания стационарных процессов, целесообразно пользоваться так называемыми структурными функциями - адекватными математическими характеристиками нестационарных случайных процессов, обладающих стационарными приращениями.
Для случайного процесса x(l), приращения которого определяются как
![]() ,
(2.1)
,
(2.1)
выражение структурной функции D(τ) имеет следующий вид:
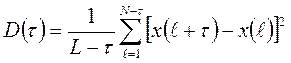 .
(2.2)
.
(2.2)
Здесь L – длина реализации; τ = 0,1,2,3,4…
Если процесс x(l) обладает стационарными приращениями, то структурная функция определяет общий второй момент разностей и является такой же важной характеристикой, как и корреляционная функция для теории стационарных процессов.
Структурная функция по своему определению всегда не отрицательна, чётная и равна нулю при τ = 0. В отличие от корреляционной функции, которая является всегда ограниченной, структурная функция может неограниченно возрастать.
Для нестационарных случайных процессов со стационарными приращениями вида (2.1) функция D(τ) не зависит от времени. Установим типы нестационарностей, относительно которых структурная функция инвариантна.
Полагаем, что нестационарный случайный процесс x(t) представляет собой аддитивную смесь стационарного случайного процесса x0(t) с нулевым математическим ожиданием и изменяющейся по некоторому закону функция f(t). Рассмотрим три типа функции f(t), а именно: линейную, квадратичную и периодическую. Принимаем
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.