Теоретическая механика. Предмет и его место в ряду других наук. Структура механики, страница 32

т.е. матрица абсолютного вращения тела равна произведении матриц относительного и переносного вращений. Составляющие же матрицы выражаются через соответствуюие эйлеровы углы, являющиеся заданными функциями времени. Тем самым функциями времени будут компоненты и абсолютной матрицы: .

По элементам абсолютной матрицы поворотов

,,,

,

эйлеровы углы в интервалах их изменения , ,  однозначно определяются

,    ;

;

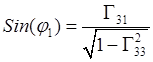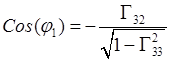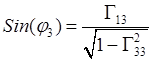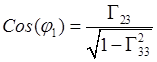,    .                                                                     (20.10)

Итак, формулы (20.8), (20.10) определяют уравнения абсолютного движения тела:  по уравнениям его относительного и переносного движений. Рассмотренную задачу называют сложением движений тела.

2°. Сложение угловых скоростей тела.

При сложном движении точки между ее абсолютной, относительной и переносной скоростями существует определенная зависимость, выражаемая теоремой сложения скоростей. Оказывается, что при сложном движении твёрдого тела аналогичная зависимость существует и между угловыми скоростями тела в составляющих и результирующем движениях. Эту зависимость выражает следующая теорема, называемая теоремой сложения угловых скоростей.

Теорема: “Если твердое тело совершает сложное движение, то в каждый момент времени его абсолютная угловая скорость равна векторной сумме переносной и относительной угловых скоростей”

.                                                                                                                     (20.11)

Доказательство. Рассмотрим типичную точку тела . При сложном движении тела  эта точка также совершает сложное движение. По теореме сложения скоростей ее абсолютная скорость складывается из переносной и относительной скоростей:

.                                                                       (20.12)

Согласно выражению скорости точки тела каждый из этих векторов определяется формулой:

,   ,   .       (20.13)

Между вектор-радиусами точки  относительно центров  и  существует зависимость  (Рис.46), с помощью которой переносную скорость можно представить в виде

.                                                                                                (20.14)

Подставив выражения скоростей согласно (20.3) и (20.14) в формулу (20.12), после перегруппировки членов получим соотношение

.                                                              (20.15)

Это соотношение можно упростить. Действительно, если воспользоваться теоремой сложения скоростей для полюса :  и воспользоваться выражением переносной скорости , то получим

.

В силу этого равенства в (20.15) часть членов сокращаются, а оставшиеся члены можно представить в виде

.

Так как  является произвольной точкой тела, то ее вектор-радиус  может быть произвольным вектором. Тогда для выполнения предыдущего равенства должен равняться нулю вектор, стоящий в квадратных скобках: . Полученное равенство и доказывает теорему.

С геометрической точки зрения теорема сложения угловых скоростей означает, что абсолютная угловая скорость тела является замыкающей ломаной линии, звеньями которой служат его переносная и относительная угловые скорости (правило треугольника угловых скоростей (Рис.47)).

Геометрическое представление позволяет устанавливать зависимости между модулями угловых скоростей и углами, которые они образуют друг с другом. Например, при известных величинах  и  модуль абсолютной угловой скорости может быть определен из треугольника угловых скоростей по теореме косинусов

.

Для аналитического вычисления абсолютной угловой скорости достаточно найти ее компоненты в подвижных или неподвижной системах отсчета.

Представим, например, угловые скорости  в базисе  подвижной системы , связанной со средой:

,    ,    .

Подстановка этих выражений в формулу для угловых скоростей (20.11) приводит к равенству

, из которого компоненты абсолютной угловой скорости тела в сопутствующей системе, связанной со средой, определяются в виде