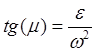Теоретическая механика. Предмет и его место в ряду других наук. Структура механики, страница 27

.                                                                                                                      (17.16)

Ускорение точки  вращающегося тела можно вычислять также как в подвижной, так и в неподвижной системе координат. В подвижной системе  для ускорения (17.13) (где ) компоненты, модуль и направление ускорения с учетом (17.5), (17.6), (17.8) определяются формулами

,

,

;                                                                                             (17.17)

,    ,    ,    .

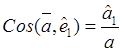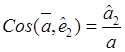Аналогично, в неподвижной системе  компоненты, модуль и направление ускорения (17.13) (с ) при учете (17.5), (17.6) и формул

,    ,   ,  

определяются в виде

,

,

                                                                                              (17.18)

,    ,    ,    .

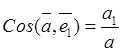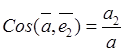Равенство нулю третьих компонент ускорения в (17.17) и (17.13):  означает, что ускорение точки ортогонально оси вращения тела, т.е. принадлежит плоскости окружности  точки.

5°. Торможение маховика.

Маховик (цилиндрическое тело) вращается замедленно вокруг своей оси так, что угловое ускорение по величине пропорционально квадрату угловой скорости .

Определить, через сколько оборотов его угловая скорость  уменьшится в два раза.

Векторное равенство  проектируем на ось вращения : . Так как 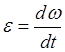, то для угловой скорости получаем дифференциальное уравнение

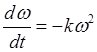. Поскольку 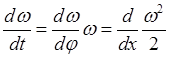, то дифференциальное уравнение можно представить в виде линейного уравнения для функции : 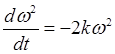. После разделения переменных получаем уравнение 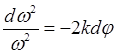, которое надо решать при условиях: , ; и , 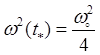. В результате интегрирования уравнения, последовательно находим

,     ,     .

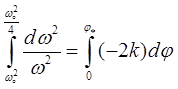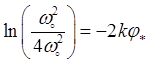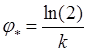Отсюда следует, что искомое число оборотов  равно: .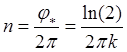

Глава3  Сложное движение тела.

Движение твердого тела называют сложным, если оно одновременно участвует в нескольких движениях. Слагаемые движения называют также составляющими движениями, а сложное движение – результирующим движением. Определение результирующего движения по составляющим движениям называют сложением движений, а определение одного из составляющих движений по результирующему и другому составляющему движению – разложением движений.

18. Относительное, переносное и абсолютное движения.

1°. Основные понятия.

Наряду с основным телом отсчета  и движущимся телом  рассмотрим некую движущуюся среду  (трактуемую как твердое тело). Свяжем с телом  “неподвижную” систему отсчета  с базисом , а с телами  и  – подвижные системы отсчета  и  соответственно с базисами  и  (Рис.38).

Движение тела  относительно среды  (в системе ) называют относительным, а по отношению к телу  (в системе ) – абсолютным. Движение же среды  относительно тела  (в системе ) – переносным.

Проиллюстрируем эти понятия следующим примером.

Пусть пассажир  движется по автобусу , который, в свою очередь, движется по Земле  (Рис.39). Свяжем с землей неподвижную систему отсчета , а с автобусом – подвижную систему . В этом случае движение пассажира  относительно автобуса  – относительное, а относительно Земли  – абсолютное. Движение же автобуса  по Земле – переносное.

Для введения характеристик различных движений тела введем важные понятия об относительной и абсолютной производных по времени от вектора.

2°. Относительная и абсолютная производные от вектора.

Рассмотрим некоторый переменный вектор , определенным в точке  среды  и представленный в базисе  системы , связанной со средой:

.                                                                                                            (18.1)

Изменение этого вектора со временем по отношению к различным (движущимся друг относительно друга) системам координат будет происходить вообще по различным законам. Различными будут и производные, характеризующие темпы этих изменений. Таким путем приходим к представлению о производных по времени от вектора в разных смыслах.

Темп изменения вектора  в неподвижной системе  выражается обычной (абсолютной) производной по времени, обозначаемой через . Согласно представлению (18.1) вектора она будет равна