Теоретическая механика. Предмет и его место в ряду других наук. Структура механики, страница 17

Эти формулы называют кинематическими формулами Эйлера (первого типа). Они позволяют определить угловую скорость тела в по уравнениям вращения тела вокруг полюса  относительно подвижных осей:

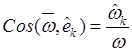
,     .                                                               (11.9)

Вектор угловой скорости можно представить и в базисе неподвижных осей :

.                                                                                                    (11.10)

Представляя в этом базисе согласно Рис.21 векторы :

,

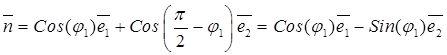, внесем их в (11.5) и после группировки членов с одинаковыми ортами получим

(11.11)

Из разложений (11.10) и (11.11) вектора  в одном и том же неподвижном базисе следует равенство одноименных компонент

,

,

                                                                                                             (11.12)

или

,    .

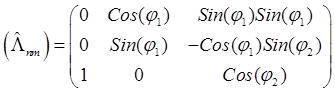Формулы (11.12) называют кинематическими формулами Эйлера (второго типа). Они также позволяют вычислить угловую скорость тела по уравнениям его вращения :

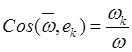
,      .                                                      (11.13)

Ранее было установлено, что вращательная часть движения тела, характеризуемая эйлеровыми углами, от выбора полюса не зависит. Поскольку в силу (11.8) (или (11.12)) угловая скорость тела определяется эйлеровыми углами, то она также не зависит от выбора полюса.

Отметим, что угловую скорость можно вводить только для абсолютно твердого тела. Для деформируемого тела можно говорить только об угловой скорости вращения малой окрестности каждой его точки. Для окрестностей различных точек угловые скорости вообще различны

3°. Формулы Пуассона.

В отличие от постоянных ортов неподвижных осей : . Орты сопутствующих осей  за счет вращения тела меняются со временем . Установим выражения для производных по времени от этих величин.

Исходим из формулы (11.4), представленной с учетом (11.5) в виде

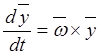.                                                                                                                     (11.14)

Представляя  в базисе подвижных осей и учитывая постоянство его компонентов в этом разложении, будем иметь

,        .

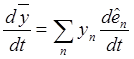
Внося эти величины в (11.14) и группируя члены с , последовательно получим

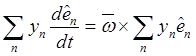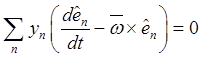,                                                        (11.15)

Вектор  является относительным вектор-радиусом типичной точки  тела: , координаты  которой могут быть произвольными величинами; поэтому для выполнения равенства (11.15) должны равняться нулю коэффициенты при них. В результате получаем равенства

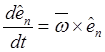
    ,                                                                                             (11.16)

называемые формулами Пуассона.

4°. Угловое ускорение тела.

Угловая скорость тела, определяемая эйлеровыми углами, изменяется со временем . Введем величину, характеризующую темп этого изменения. Рассмотрим пространство годографа угловой скорости .

В соседние моменты времени  и  угловая скорость имеет значения , , определяющие положения ,  точки, вычерчивающей годограф  (Рис.22).

Следовательно, за промежуток времени  угловая скорость получает приращение , направленное по хорде  годографа.

Отношение 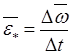 называют средним угловым ускорением за время . Вектор  направлен по хорде . Среднее угловое ускорение является приближенной величиной. Однако это приближение тем точнее, чем меньше . Поэтому за угловое ускорение тела в момент  принимают предел , к которому стремится  при стремлении к нулю приращения времени, т.е.

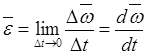.                                                                                                           (11.17)

Таким образом, угловое ускорение тела есть векторная величина, равная производной по времени от угловой скорости. Так как при  направление хорды  определяет направление касательной к годографу  в точке , то угловое ускорение направлено по касательной к годографу угловой скорости (Рис.22).

Если представить угловую скорость тела через скорости прецессии, нутации и собственного вращения, то для углового ускорения получим выражение