х"-1: х™ - 2хс ~х"~\ Если fix**) <f(xnA), то принять хпА = л:*"'1 и перейти к шагу 2. Иначе - перейти к шагу 6. Шаг 6. Перейти к новому правильному симплексу с вдвое меньшим ребром, считая базовой вершиной х°. Остальные « вершин симплекса найти по формулех - (х1 + х)/2, i - 1,.., п. Перейти к шагу 1.
Геометрическая иллюстрация работы алгоритма в пространстве Ег показана на рис.4.2, где точки х°, х\ х2 вершины начального симплекса, а пунктиром указаны процедуры отражения.
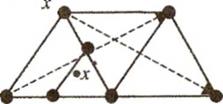
Рис.4.2. Поиск точки минимума функции f(x) с помощью правильных симплексов в пространстве Ег
5. Методы безусловной минимизации, использующие производные функции
Пусть функция f(x) дифференцируема в Е„. В этом случае алгоритмы поиска минимума функции основаны на следующих зависимостях хк=хк-*+акрк, к=\,..., х°еЕ„, (5.1)
где рк - направление поиска точки / из х тем или иным способом с учетом информации о частных производных функции ffx);
Ofc - величина шага, которую выбирают так, чтобы выполнялось условие
/(**)</(**-'), к =1,2,... (5.2)
Так как функция предполагается дифференцируемой, то в качестве критерия останова в случае бесконечной итерационной последовательности fxrj, как правило, выбирают условие
\f\xk%<8 (5.3)
Теорема 5.1. Для квадратичной функции ffx) = <Ах, х + + <Ь, х> + с величина а* исчерпывающего спуска в итерационном процессе будет
_ </'(**,/> <Ах* + Ь,р'>
<W> <Ар\р'> (5-4)
5.1. Метод градиентного спуска
Примем в (5.1) на каждом шаге рк -f'(xk). Если ff(xk)^0, то направление вектора р является направлением убывания функции f(x), причем в малой окрестности точки jr* направление рк обеспечивает наискорейшее убывание этой функции. Поэтому можно найти такое а* >0, что будет обеспечено выполнение условия (5.2).
Приведем алгоритм одного из вариантов метода градиентного спуска.
Шаг 0. Задать параметр точности е 0, начальный шаг а 0, выбрать хеЕ„. Вычислить f(x).
Шаг 1. Найти f'(x) и проверить условие достижения точности (5.3). Если оно выполнено, вычисления завершить, полагая х - х, f - f(x). Иначе - перейти к шагу 2.
Шаг 2. Найти у = х - ctf'fx) и f(y). Если f(y) f(x), го принять х =у, f(x) - f(y) и перейти к шагу 1. Иначе - перейти к шагу 3. ШагЗ. Принять а а/2 и перейти к шагу 2.
Вблизи стационарной точки функции f(x) величина |/'(*)||
становится малой. Это может приводить к замедлению сходимости последовательности {хк}. Поэтому иногда в (5.1) полагают
рк =-/'(**)/ /'(•**)L т.е. вместо -ffx) используют вектор
(5.6) и (5.8) получаем ||х* - х'\ < qbf 1 - х
, т.е.
единичной длины того же направления.
Приведем теоретическое обоснование сходимости градиентного метода с постоянным шагом <% & а
\х ~х
<
q \\х -х
 |
|
х |
|
X |
Cf(x>) (5.5)
и получим оценку скорости сходимости при минимизации выпуклой квадратичной функции ffx) = <Ах, х> + <Д х> +■ с.
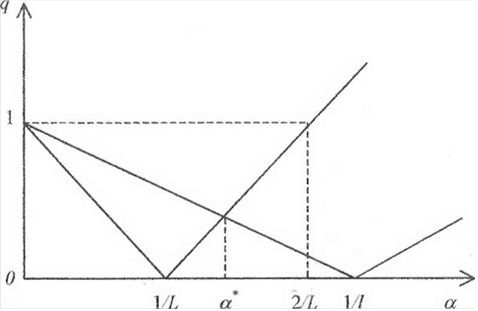
Теорема 5.2. Пусть симметрическая матрица А квадратичной функции f(x) положительно определена, / и L - ее наименьшее и наибольшее собственные значения (0 < I <Ь). Тогда при любых ае(0; VL) и х°еЕ„ итерационная последовательность (6.5) сходится к единственной точке глобального минимума х функции ffx) линейно (со скоростью геометрической прогрессии):
p-/||<^||jc°-/| , (5.6)
где q = max|l - al\, |l - al\}.
Так как матрица А положительно определена, функция f(x) сильно выпукла и, следовательно, точка х существует и единственна. Градиент ffx) в этой точке обращается в нуль, т.е. ffx) = Ах* + Ъ - 0. Для точкихк имеем: ffx) - Ахк + b = Ах* + Ь-Ах - b = А(хк - х*). Оценим норму разности
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.