Промышленность \ Физикохимия и механика композиционных материалов

Методы оптимизации композиционных систем, страница 7

х,:

дх2 дх*

Шаг 1. Запишем систему (3.5)

2х

- 2..г, - 2-х,.

Согласно необходимому условию минимума

1

=>12 =

2х} -1 = 0 2х2-х3=0 2 л3 - 2 - х2

Решив систему, получим стационарную точку х

Шаг 2. Находим гессиан 2    0    0

2


I 1 1 2*3*3


4. Прямые методы безусловной минимизации

Рассмотрим конкретные вычислительные алгоритмы решения задачи безусловной минимизации f(x)-#nin, хеЕ„, которые основаны только на вычислении значений функции f(x), т.е. прямые методы минимизации. Важно отметить, что для их применения не требуется не только дифференцируемости целевой функции, но даже аналитического ее задания. Нужно лишь иметь возможность вычислять или замерять значения f(x) в произвольных точках. Такие ситуации часто встречаются в практически важных задачах оптимизации.

4.1. Минимизация методом правильного симплекса

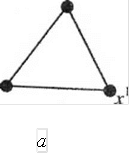
Правильным симплексом в пространстве Е„ называется множество из п + / равноудаленных друг от друга точек (вершин симплекса). Отрезок, соединяющий две вершины, - ребро симплекса.

В пространстве Ег правильным симплексом является совокупность вершин равностороннего треугольника, в Ез - правил! лого тетраэдра.

Если х1 - одна из вершин правильного симплекса в £"„, то координаты остальных п вершин х!,... ,х" можно найти по формуле


24


25


(4.1)

где d{ = a[jn + \ - l)/ ид/2; J2 = a{y/n +1 + л -1)/«>/2; л - длина ребра. Вершину jc симплекса, построенного по формулам (4.1), будем называть базовой.

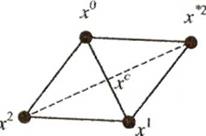
В алгоритме симплексного метода используют следующее важное свойство правильного симплекса. По известному симплексу можно построить новый симплекс путем отражения какой-либо вершины, например, х симметрично относительно центра тяжести хс остальных вершин симплекса. Новая и старая вершины х и хк связаны соотношением

х , где х'

хч+х*

2

iv '

nLx ■  в результате получается новый правильный симплекс с тем же ребром и вершинами х = 2хс - х\ х, i 0,... ,п, \Л. Таким образом, происходит перемещение симплекса в пространстве Е„. На рис.4.1 представлена иллюстрация этого свойства симплекса в пространстве Ег.

х°

б

?vEl 01ражением тат

Центр отражения ^'jZtf

Поиск точки минимума функции /ft) с помощью правильных симплексов производят следующим образом. На каждой итерации сравнивают значения f(x) в вершинах симплекса. Затем выполняют описанную выше процедуру отражения для той вершины, в которой f(x) принимает наибольшее значение. Если в отраженной вершине получается меньшее значение функции, то переходят к новому симплексу. В противном случае выполняют еще раз процедуру отражения для вершины со следующим по величине значением/ft). Если и она не приводит к уменьшению функции, то сокращают длину ребра симплекса, например, вдвое, и строят новый симплекс с этим ребром. В качестве базовой выбирают ту вершину х старого симплекса, в которой функция принимает минимальное значение. Поиск точки минимума/ft) заканчивают, когда либо ребро симплекса, либо разность между значениями функции в вершинах симплекса становятся достаточно малыми.

Опишем один из вариантов алгоритма этого метода. Шаг 0. Выбрать параметр точности s, базовую точку х , ребро а и построить начальный симплекс по формулам (4.1). Вычислить

кЛ

Шаг 1. Определить   значения /ft)   в   вершинах   симплекса х\ ... ,х".

Шаг 2. Упорядочить вершины симплекса х , ...х" так,   чтобы /ft0) <f(xx) <... <f(x"x) <f(x"). Шаг 3. Проверить условие

-±[fH~fHl<*2-                                                                 (4-2)

п м

Если оно выполнено, то вычисления прекратить,             полагая х &x°tf -f(x°), В противном случае перейти к шагу 4.

Шаг 4. Найти хе=-Ул'и произвести отражение вершины п ш

х":х*" 2хс х". Еслиf(x*) /ft";, то принятьх" /" и перейти к шагу 2. Иначе   перейти к шагу 5.

Шаг 5. Найти jcc =— V*1 и выполнить отражение вершины

п ш-\

Скачать файл