Методы оптимизации композиционных систем, страница 12

1.  Задача линейного программирования - в (6.2) - (6.4) все функции /(*),& (х) - линейны, и все переменные x_f удовлетворяют условию отрицательности х. > О.

2.  Задача нелинейного программирования - хотя бы одна из функций f{x\ g_t(x) в (6.2) - (6.4) не является линейной.

3.  Задача на условный экстремум - отсутствуют ограничения-неравенства (6.3), т.е. У, = 0.

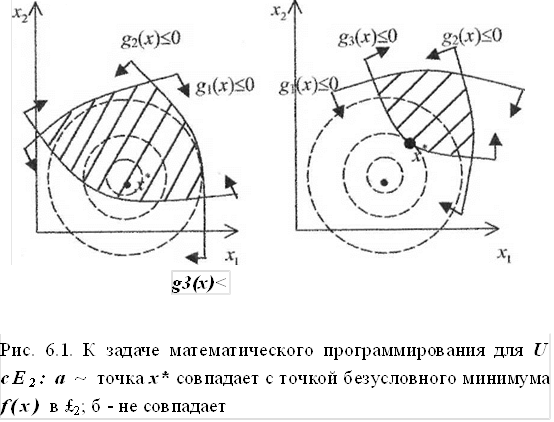
4.   Задача выпуклого программирования - все функции f(^x\gti^x) ^в (⁶*²) ~ (б-⁴) - выпуклы, а ограничения-равенства отсутствуют, т.е. 1₂ - 0. Ее допустимое множество U- выпукло.

Решение задач математического программирования, как правило, связано со значительно большими трудностями, чем решение задач безусловной минимизации. На рис. 6.1 приведены возможные случаи расположения точки минимума х в задаче математического программирования /(*)-» min, #Дх)<0, i -1,2,3, х е Е₂ на допустимом множестве U (множество U заштриховано). Пунктиром изображены линии уровня целевой функции.

Основной принцип действия этой группы методов состоит в преобразовании задачи нелинейного программирования f(x)-*min,xe U в последовательность задач безусловной минимизации

f_k(x)=f(x)+p_k(x)-* min, х е Е„₉ к = 1,2,...,                           (6.5)

где Ф_к\х) - функции, которые с ростом к во все большей степени учитывают ограничения, определяющие допустимое множество U исходной задачи.

В качестве приближенного решения исходной задачи принимают решение х вспомогательной задачи (6.5), соответствующее достаточно большому значению к.

6.2.1. Метод штрафных функций

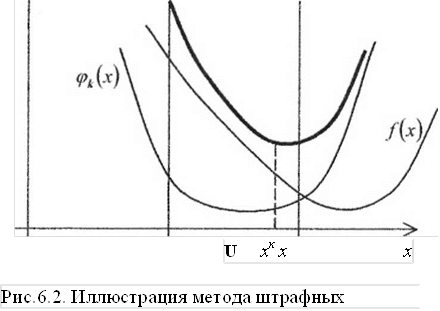
В этом методе функции <р_к(х) подбирают так, чтобы при больших к функция f_k(x) из (6.5) мало отличалась от f(x) при хеС/ и быстро возрастала при удалении точки х £ U от допустимого множества. Идею метода штрафных функций иллюстрирует рис. 6.2, соответствующий, для наглядности, одномерному случаю.

Пусть U е Е_л - заданное множество. Последовательность функций {(р_к(л)}, определенных в Е_п и обладающих свойством

, ч   [0, если х е U.

\™<РЛ^Х) = \                                                                        (6-6)

[со, если х <£ (У, называется последовательностью штрафных функции множества U.

Пусть {Л_к} - какая-либо возрастающая числовая последовательность с положительными членами и lim Д. = -нх>, а функция

к—>эо

<р(х) обращается в нуль при л- е U и принимает положительные значения при х £ U. Тогда последовательность (р_к (х) = А_к(р(х) удовлетворяет условию (6.6).

На практике часто полагают А_к = к,к- 1,2,...

В качестве функции <р(х) можно взять, например, p(xjj) -расстояние от точки х до множества 11. Тогда последовательность штрафных функций примет вид

<р_к(х)=кр(хЛ1).                                                                (6.7)

Вычисление расстояния p(x₉U)₉ а, следовательно, и значений штрафной функции A_kp\x,U) может быть затруднительным, поэтому часто применяют штрафные функции более удобного вида с учетом явного задания границ множества U. Пусть множество U задано неравенствами

_gi(.x)<0, i = l,...,/w,                                                                (6.8)

где g,(xj - выпуклые функции. Тогда в качестве (р{х) в выражении (p_k{x)= А_к<р(х) можно взять

т

р(*)=1М&М),

i=I

где y/{i) - непрерывная функция, причем = 0, если / < 0 и \l/{t) > 0 при t > 0. Если lim А,, = +со и А > 0, то для последовательности {^(х)}, #>Дх) =              условия (6.6) выполняются, т.е. она является последовательностью штрафных функций. Функцию yr(i) можно выбрать так, чтобы функции <р_к (х) обладали свойствами, упрощающими решение вспомогательных задач мини-цзации (6.5), например, такими, как выпуклость, существование производных, простота вычислений и т.д. Часто полагают

*W-£k*«f.                                                                (6.9)

ы

где g; (х) = max{0, g, (х)} = -(g, (х) +1 g, (х) |).