Метод сил, страница 9

d k1 X1  + ... + d kk X k  + d kk +1 X k +1  + ... + d kn X n  + D kP  = 0

d k +11 X1  + ... + d k +1k X k  + d k +1k +1 X k +1  + ... + d k +1n X n  + D k +1P  = 0

...........................................................................

d n1 X1  + ... + d nk X k  + d nk +1 X k +1  + ... + d nn X n  + D nP  = 0

(8.22)

Кроме того, трудоемкость расчета методом сил зависит от числа со- вместно  решаемых  уравнений  для  определения  основных  неизвестных. Число  совместно  решаемых  канонических  уравнений  зависит  от  выбора

варианта  основной  системы  метода  сил.  Следует  различать  следующие возможные разновидности основных систем метода сил.

Во-первых, обычная основная система, когда для определения основных неизвестных нужно совместно решать все n канонических уравне- ний системы (8.22). Такой вариант решения канонических уравнений явля- ется самым неблагоприятным.

Во-вторых, идеальная  основная система,  когда система  канониче- ских  уравнений  распадается  на  n  отдельных  уравнений,  содержащих  по одному неизвестному

d11 X1  + ................................................. + D1P  = 0

..........................................................................

.....................d kk X k  + ............................. + D kP  = 0

..................................d k +1k +1 X k +1  + ........ + D k +1P  = 0

...........................................................................

.....................................................d nn X n  + D nP  = 0

(8.23)

Каждое  уравнение  (8.23)  позволяет  независимо  найти  соответствующее основное  неизвестное.  Такой  вариант  решения  канонических  уравнений является наиболее благоприятным. В принципе, приведение системы кано- нических уравнений к виду (8.23) возможно для любой статически неопре- делимой стержневой конструкции.  В общем случае трудоемкость процесса  приведения  канонических  уравнений  к  виду  (8.23)  достаточна  велика.

Однако существуют приемы, позволяющие для статически неопределимых стержневых конструкций частного вида, достаточно просто получать идеальные основные системы метода сил [    ].

В-третьих, рациональная основная система, когда система канонических уравнений распадается на две отельные подсистемы уравнений

d11 X1  + ... + d1k X k  + ................................ + D1P  = 0

..............................................................................

d k1 X1  + ... + d kk X k  + ................................ + D kP  = 0

................................d k +1k +1 X k +1  + ... + d k +1n X n  + D k +1P  = 0

...........................................................................

................................d nk +1 X k +1  + ... + d nn X n  + D nP  = 0

Первая  подсистема  уравнений  содержит  основные  неизвестные

(8.24)

X1 ,..., X k ,

вторая -

X k +1 ,..., X n  . Поэтому решение системы канонических уравнений в

виде (8.24) позволяет, не сокращая числа неизвестных, найти их независимо по частям.

Одним из приемов получения рациональной основной системы является  использование  свойств  симметрии  рассчитываемой  статически  неоп- ределимой  стержневой  конструкции.  В  строительной  механике  использу- ется  понятие  геометрической  или  пространственной  симметрии,  согласно

которому конструкция должна быть инвариантна относительно геометрических преобразований – поворота вокруг оси или отражения в плоскости.

Поэтому  признаками  симметрии  стержневой  конструкции  относительно некоторой оси являются:

-   симметрия общих геометрических размеров;

-   симметрия схем узловых соединений и опорных закреплений;

-   симметрия  жесткостных  характеристик  конструктивных  элементов.

8.3.2. Расчет симметричных систем частного вида

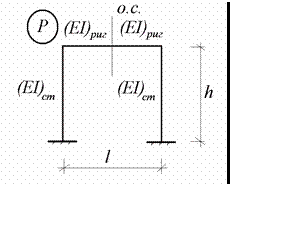
Рассмотрим одноэтажную однопролетную раму (рис.8.4)

Рис.8.4

удовлетворяющую все признакам симметрии и обладающую осью симмет- рии. На раму действует произвольная нагрузка, показанная на рис.8.4 ус- ловным буквенным обозначением P .

Рассматриваемая рама три раза статически неопределимая система