Основы теории электромагнитного поля. Направленные электромагнитные волны и направляющие системы, страница 17

В волновых процессах в отличие от гармонических колебаний фаза колебаний зависит не только от времени t, но и от удаления точки от источника волн и скорости распространения электромагнитных колебаний.

Гармонические колебания

                                                                         (4.1)

Волновой процесс

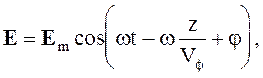                                                                     (4.2)

где z - координата рассматриваемой точки, V_ф - фазовая скорость волны.

В зависимости от формы фазового фронта волны - формы поверхности, во всех точках которой векторы поля имеют одну и ту же фазу, волны подразделяются на плоские

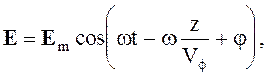                                                                    (4.3)

цилиндрические

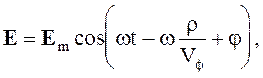                                                                     (4.4)

сферические

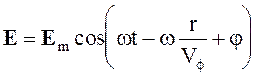,                                                                      (4.5)

В этих выражениях z, r, r - координаты декартовой, цилиндрической, сферической систем координат, в направлении которых распространяется волна.

На большом расстоянии от источников фазовый фронт любой волны в пределах достаточно большого участка можно считать плоским, поэтому волнам на больших расстояниях от источника присущи свойства плоской волны. Благодаря этому факту, наибольший интерес представляет изучение свойств плоских волн.

Кроме поверхности равных фаз при рассмотрении волновых процессов вводится также понятие поверхности равных амплитуд. В случае совпадения поверхностей равных фаз и равных амплитуд волна называется однородной. Если поверхность равных фаз на совпадает с поверхностью равных амплитуд волна называется неоднородной. Всегда можно представить неоднородную волну, распространяющуюся в определенном направлении, в виде совокупности однородных волн.

4.1. Волновые уравнения для монохроматического электромагнитного поля и их решения.

Решение уравнений электромагнитного поля обычно производят после их представления в виде волновых уравнений - дифференциальных уравнений в частных производных второго порядка.

Преобразуем уравнения

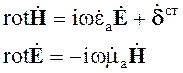
Для этого применим к обеим частям первого уравнения операцию rot и получим

                                                                  (4.6)

Из второго уравнения подставим в (4.6) значение

Получим

                                                                 (4.7)

Используя известное тождество

получаем с учетом, что  для однородной изотропной среды

                                                                                 (4.8)

где  - волновое число, - оператор “набла”.

Получим аналогично волновое уравнение для вектора

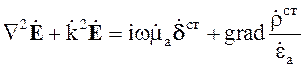                                                           (4.9)

Обычно решают одно из волновых уравнений (4.8) или (4.9), определяют вектор , а затем находят второй вектор с помощью уравнений электромагнитного поля. Так как наибольший интерес представляют плоские волны, будем искать решение волнового уравнения для плоских однородных волн.

В той части пространства, где отсутствуют сторонние токи и сторонние заряды, волновые уравнения принимают вид

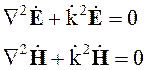                                                                                   (4.10)

и называются однородными волновыми уравнениями. Они описывают свободное, существующие без источников гармоническое электромагнитное поле.

Описание плоских волн удобнее всего производить в декартовой системе координат. При распространении возбуждения, вызываемого волновым процессом, вдоль оси z фазовый фронт волны перпендикулярен оси z, то есть является плоскостью xOy. Так как рассматривается волна плоская однородная, то во всех точках плоскости xOy амплитуды и фазы векторов E и Н одинаковы. Следовательно производные по координатам x и y будут равны нулю и волновое уравнение, записанное в декартовой системе координат для вектора

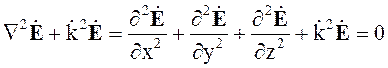
принимает вид

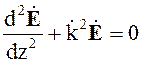                                                                                    (4.11)

Векторное уравнение (4.11) записывается в виде

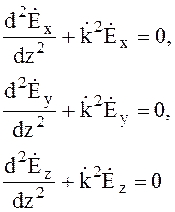                                                                            (4.12)