Алгебра векторов, страница 9

2. (а + b) + с = а + (b + с);

3. Для любого вектора а выполняется равенство а + 0 = а.

4. Для любого вектора а существует противоположный вектор - а  такой, что а + (-а) = 0.

5. 1.;

6. ;

7. ;.

8. Для  выполняется равенство .

            Векторными пространствами являются:

            V¹ – множество векторов, расположенных на прямой;

            V² – множество векторов, расположенных на плоскости;

            V³ – множество векторов, расположенных в пространстве.

            Опр. 1.5.2. Базисом векторного пространства называется любая линейно независимая упорядоченная система векторов такая, что любой вектор пространства является линейной комбинацией векторов этой системы.

            Опр. 1.5.3. Размерностью векторного пространства называется количество векторов в его базисе.

            Сформулируем ряд утверждений, основывающихся на теоремах 1.4.6 - 1.4.8 и следствиях из них, касающихся базисов и размерностей пространств V¹ , V² и V³.

1. Базисом пространства V¹ векторов, расположенных на прямой, является любой ненулевой вектор.  Размерность пространства V¹ равна 1.

2. Базисом пространства V² векторов, расположенных на плоскости, является любая пара некомпланарных векторов.  Размерность пространства V² равна 2.

3. Базисом пространства V³ векторов, расположенных в пространстве, является любая тройка некомпланарных векторов.  Размерность пространства V³ равна 3.

Согласно определению 1.5.2, любой вектор пространства может быть представлен в виде линейной комбинации векторов базиса. Рассмотрим для примера пространство V³. Пусть е₁, е₂, е₃ - базис этого пространства. Тогда любой вектор  представляется в виде  . Такое представление называется разложением вектора а по базису е₁, е₂, е₃, а числа х₁, х₂, х₃ - координатами вектора а в базисе е₁, е₂, е₃. Вектор а с координатами х₁, х₂, х₃ в базисе е₁, е₂, е₃ будем записывать и в форме , и форме а(х₁, х₂, х₃). Докажем, что координаты вектора определяются однозначно.

Теорема 1.5.1. Разложение вектора по базису единственно (другая формулировка: равные векторы имеют равные координаты).

            Док-во. Предположим, что имеется два разложения вектора а по базису е₁, е₂, е₃:  и . Тогда , или . Векторы базиса линейно независимы, следовательно их линейная комбинация дает нуль-вектор только в тривиальном случае: 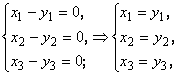 что и требовалось доказать.