Алгебра векторов, страница 2

В прикладных науках (физике, механике и т.д.) применяют другие разновидности векторов, отличные от свободных. Так, вектор называют скользящим, если он может быть перенесен вдоль прямой, на которой он лежит (в этом случае два вектора равны, если они имеют равные длины, одинаково направлены и лежат на одной прямой). Скользящим является вектор угловой скорости вращающегося тела. Вектор называется закрепленным (или приложенным), если он определяется не только длиной и направлением, но и точкой приложения. Закрепленным является вектор силы, действующей на упругое тело. Для закрепленных векторов не вводится понятие равенства, т.е. каждый закрепленный вектор равен только самому себе. Естественно, понятие математического вектора – наиболее общее; так, при решении задач каждый скользящий или закрепленный вектор может быть представлен в виде разности двух свободных векторов.

Опр. 1.1.7. Ортом, или единичным вектором, называется вектор, длина которого равна единице.

Опр. 1.1.8. Ортом вектора а называется единичный вектор, сонаправленный с вектором а. Орт вектора а будем обозначать а₀.

Опр. 1.1.9. Вектор, имеющий одинаковый модуль с вектором а и противонаправленый ему, называется противоположным вектору а. Вектор, противоположный вектору а, обозначается символом -а. Если , то .

1.2. Линейные операции над векторами.

Под линейными операциями над векторами понимаются операции сложения (вычитания) векторов и умножения вектора на скаляр (число).

Опр. 1.2.1. (Правило треугольника). Суммой векторов а и b называется вектор с = а + b, соединяющий начало вектора а с концом вектора b, если начало вектора b совмещено с концом вектора а .

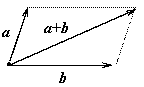Опр. 1.2.2. (Правило параллелограмма). Суммой векторов а иb, имеющих общее начало, называется вектор, равный по длине и параллельный диагонали параллелограмма, построенного на векторах а и b, и выходящей из общего начала векторов а и b.

 Очевидно, эти определения эквивалентны, т.е. определяют один и тот же вектор с = а + b.

Теорема 1.2.1. Операция сложения векторов обладает следующими свойствами:

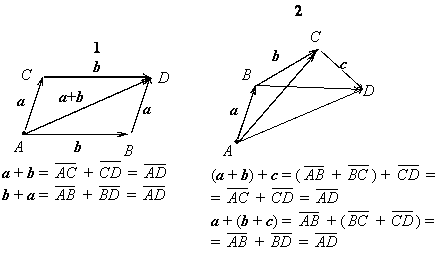
1. а + b = b + а для любых векторов  а, b (коммутативность);

2. (а + b) + с = а + (b + с) для любых векторов  а, b, с (ассоциативность);

3. Для любого вектора а выполняется равенство а + 0 = а.

4. Для любого вектора а существует противоположный вектор - а  такой, что а + (-а) = 0.

Справа приведены рисунки, иллюстрирующие доказательства первого и второго свойств. Третье и четвертое свойства очевидны:

3. а + 0 = ;

4. Если , и взять , то а + (-а) =  = 0.