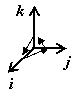Алгебра векторов, страница 19

            1.7.4. Вычисление векторного произведения в правом ортонормированном базисе. Пусть i,j, k – базисные орты. Из картинки справа убеждаемся, что [i, j] = k; [j, k] = i; [k, i] = j. Кроме того, [j, i] = - k; [k, j] = - i; [i, k] = - j, и [i, i] =

=[j, j] = [k, k] = 0.

Пусть а = а_х i + а_у j + а_z k и b = b_х i + b_у j + b_z k.  Тогда

[а, b] = [а_х i + а_у j + а_z k, b_х i + b_у j + b_z k] = а_х b_х [i, i] + а_х b_у [i, j] + а_х b_z [i, k] + … +
+ а_z b_z [k, k] = а_х b_у k + а_х b_z (-j) + а_у b_х (-k) + а_у b_z i + а_z b_х j  + а_z b_у (-i) =

= i (а_у b_z - а_z b_у) - j (а_х b_z  - а_z b_х) + k (а_х b_у  - а_у b_х) = .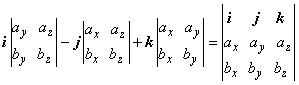

            Нами доказана

Теорема 1.7.1: Координаты векторного произведения векторов а и b равны алгебраическим дополнениям элементов первой строки символического определителя .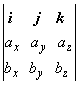

Решение типовых задач.

Пример 1 Найти площадь параллелограмма, построенного на векторахa = 3m – 2n  и

с = m – 3n, если |m| = 5, |n| = 2, .

Решение. Согласно пятому свойству векторного произведения, площадь параллелограмма равна S = | [a, c] |. Найдём векторное произведение векторов a и c: [a, c] = [(3m – 2n), (m – 3n)] =

= 3[m, m] - 9[m, n] - 2[n, m] + 3[n, n].  Учитывая, что [m, m] = [n, n] = 0, [n, m] = - [m, n], получим [a, c] = -7[m, n]. Тогда S = | -7[m, n] = 7| [m, n] | = .