Алгебра векторов, страница 22

16. Упростить выражение (a – b)x(c + 2a) + (b – 3c)x(2a + b).

17. Двойным векторным произведением векторов a, b, c называется произведение [a x [b x c]]. Доказать, что [a x [b x c]] = (ac) b – (ab) c.

1.8. Смешанное произведение трех векторов.

            Опр. 1.8.1. Смешанным произведением векторов a, b, c называется векторно-скалярное произведение ([a, b], c).

Согласно этому определению первые два сомножителя умножаются векторно, затем результат скалярно умножается на третий сомножитель.

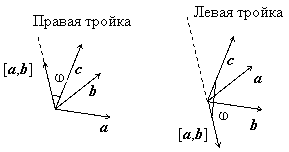
            Теорема 1.8.1 (геометрический смысл смешанного произведения). Модуль смешанного произведения векторов a, b, c равно объему параллелепипеда, построенного на этих векторах. Смешанное произведение положительно, если тройка векторов a, b, c – правая, и отрицательно, если эта тройка – левая (если векторы a, b, c компланарны, то их смешанное произведение равно нулю).

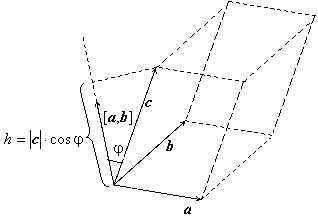Док-во. V_пар = . Справа в этом равенстве стоит модуль смешанного произведения. Знак смешанного произведения определяется знаком косинуса: если тройка a, b, c – правая, то векторы [a, b] и с расположены в одном полупространстве относительно плоскости векторов a и b, , ; если тройка a, b, c – левая, то векторы [a, b] и с расположены в разных полупространствах относительно плоскости векторов a и b, , ; если компланарны, то высота параллелепипеда равна нулю, и V_пар =0.

            Из доказанной теоремы следует, что

([a, b], c) = (a, [b, c]), так как для троек a, b, c  и

b, c, а совпадают и построенные на них параллелепипеды и ориентации (циклическая перестановка). Следовательно, при сохранении порядка сомножителей не важно, где стоят квадратные скобки, обозначающие векторное произведение. Поэтому их обычно опускают, и обозначают векторное произведение просто  или вообще abc.

            Итак, abc = саb = bcа = – bаc = – сbа =  –аcb.

     Отметим еще одно очевидное следствие из теоремы. Объем треугольной пирамиды, образованной векторами a, b, c, вычисляется по формуле .

     1.8.2. Свойства смешанного произведения.

1.  (а + b)cd = аcd  + bcd;

2.  ;

3.  (Необходимое и достаточное условие компланарности векторов) Смешанное произведение трёх векторов равно нулю тогда и только тогда, когда векторы компланарны;