Алгебра векторов, страница 24

= 5|(2a, a x c) + (b, a x c) – (c, (a x c)|. Так как смешанное произведение, в котором два одинаковых вектора, равно нулю, то V = 5|(b, a x c)|. Поскольку a x c  a, a x c  c, то a x c || b и  векторы a x c и b сонаправлены (тройка векторов - правая), угол между ними равен нулю, и . Но . Окончательно получим .

Пример 2. Найти объём треугольной пирамиды SABC, образованной векторами , ,  и длину её высоты, опущенной на грань ABS.

Решение. Объём треугольной пирамиды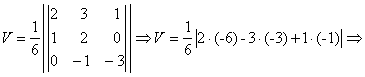

. Находим площадь ΔABC: . Найдём векторное произведение 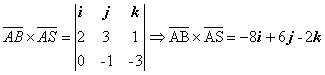, следовательно .

С другой стороны объём треугольной пирамиды находим по формуле:

.

Пример 3. Доказать, что точки А(2, 3, -1), B(1, 2, 5), C(4, 3, -3), D(3, 2, 3) принадлежат одной плоскости.

Решение. Найдем векторы , , . Точки принадлежат одной плоскости тогда и только тогда, когда векторы ,  и  компланарные. Вычислим смешанное произведение этих векторов:

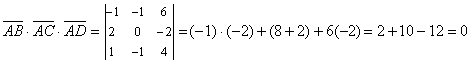. Следовательно, векторы ,  и   компланарны, то есть точки A, B, C, D принадлежат одной плоскости.

Задачи для самостоятельной работы.

1. Найти объём параллелепипеда, построенного на векторах a = m + n, b = 2p - n,

 c = p + 2n + 3m, если взаимно ортогональные векторы m, n, p  образуют левую тройку векторов и |m| = 2, |n| = 3, |p| = 2.

2. Треугольная пирамида задана радиусами- векторами своих вершин r_A = (0, 1, 2),

r_B = (1, 3, 1), r_C = (2, -2, 0) и r_S = (-4, -1, 3). Определить объём пирамиды и длину высоты, опущенной на грань ASB.

3. Показать, что точки А(1, -3, 2), B(-1, -2, 3), C(2, -5, 5), D(15, -16, 9) лежат в одной плоскости.

4. В основании четырёхугольной пирамиды SABCD лежит параллелограмм ABCD, построенный на векторах  и . Задано боковое ребро  и точка F делит сторону BS в отношении 1:2. Вычислить объём пирамиды ABDF.