Алгебра векторов, страница 10

1.5.2. Линейные операции в координатной форме.

Рассмотрим, как преобразуются координаты при сложении векторов и при умножении вектора на число.

Теорема 1.5.2. При сложении векторов их соответствующие координаты складываются.

Док-во. Пусть  и . Тогда , что и требовалось доказать.

Теорема 1.5.3. При умножении вектора на число все его координаты умножаются на это число.

Док-во. Пусть . Тогда , что и требовалось доказать.

При доказательстве обеих теорем используются свойства операций сложения векторов и умножения вектора на число, входящие в определение векторного пространства.

Следствие из теор. 1.5.3: Критерий коллинеарности векторов.  Два ненулевых вектора коллинеарны тогда и только тогда, когда их координаты в любом базисе пропорциональны.

Док-во. Необходимость. Пусть векторы а(х₁, х₂, х₃) и b(y₁, y₂, y₃) коллинеарны. Тогда по теореме 1.4.6. , т.е. .

Достаточность. Если координаты векторов пропорциональны, т.е. , то , и  .

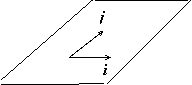1.5.3. Ортонормированный базис. Направляющие косинусы.

Опр.1.5.4. Базис векторного пространства называется ортонормированным, если составляющие его векторы взаимно перпендикулярны и имеют единичную длину.

Ортонормированный базис на плоскости обычно вводят парой ортов i, j. Прежде чем ввести ортонормированный базис в пространстве, дадим определение ориентации тройки векторов.

Опр. 1.5.5. Упорядоченная тройка некомпланарных векторов a, b, c называется правой, если при приведении этих векторов к общему началу кратчайший поворот от a к b виден из конца вектора c против часовой стрелки (если кратчайший поворот от a к b совершается по часовой стрелке, то тройка векторов a, b, c называется левой).

Заметим, что если тройка a, b, c – правая (левая), то правыми (левыми) являются тройки b, c, a и c, a, b, т.е. ориентация не меняется при циклической перестановке векторов. В тоже время перестановка двух векторов меняет ориентацию: если тройка a, b, c – правая (левая), то тройка b, a, c  (и, как следствие, тройки a, c, b и c, b,a) – левая (правая).

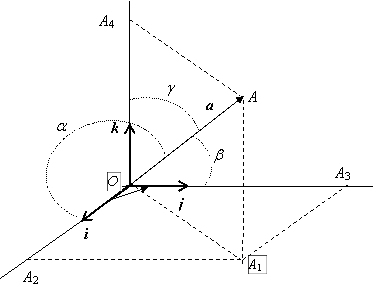
Ортонормированный базис в пространстве будем задавать правой тройкой ортов i, j, k. Произвольный вектор пространства a теперь может быть представлен в виде . На рисунке справа х = ОА₂, у = ОА₃, z = ОА₄, все три координаты положительны. Если х, у, z – координаты вектора а в ортонормированном базисе, то (док-во: |a|² = ОА² = ОА₁² + A₁А² (так как тр-к OAA₁ – прямоугольный) =  (ОА₂² + A₂А₁²) + A₁А² = ОА₂² + ОА₃² + ОА₄²).