Алгебра векторов, страница 23

4.  Смешанное произведение не меняется при циклической перестановке сомножителей: abc = = саb = bcа;

5.  Смешанное произведение меняет знак при перестановке дух сомножителей:

bаc = – аbс.

        Док-во. Первые два свойства следуют из соответствующих свойств скалярного произведения (см. пункт 1.6.2 свойства 4 и 5): (а + b)cd = (а + b, [c, d]) = (а, [c, d]) +  (b, [c, d]) =

= аcd  + bcd; ; остальные свойства обсуждались выше.

Теперь мы можем доказать второе свойство векторного произведения (см. пункт .7.2. Свойства векторного произведения): [а + b, с] = [а, с] + [b, с]. Покажем, что векторы в левой и правой частях этого равенства имеют одинаковые координаты (тогда, по теореме 1.5.1.о единственности разложения по базису, эти векторы равны). Координаты вектора равны скалярным произведениям этого вектора на базисные орты (см. пункт 1.6.3. Скалярное произведение векторов, заданных в ортонормированном базисе). Находим эти произведения: ([а + b, с], i) (это смешанное произведение, для которого свойство доказано) = ([а, с], i) + ([b, с], i) = (([а, с] + [b, с]), i) – это уже произведение для суммы векторов в правой части доказываемого равенства. Так же доказываются равенства для второй (с ортом j) и третьей координат (c k).

1.8.2. Вычисление смешанного произведения в ортонормированном базисе.

Теорема 1.8.2. Смешанное произведение abc векторов а_х i + а_у j + а_z k, b = b_х i + b_у j + b_z k,

с = с_х i + с_у j + с_z k равно определителю .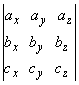

Док-во. abc = (a, [b, c]) =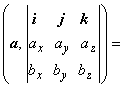

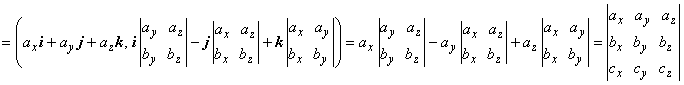
Решение типовых задач.

Пример 1. Найти объём параллелепипеда, построенного на векторах m = 2a + b – c,

n = a + 3c, p = 3a + 4c, если взаимно ортогональные векторы a, b, с  образуют правую тройку векторов и |a| = 1, |b| = 2, |c| = 3.

Решение. По теореме 1.8.1 V = |mnp| или V = |(2a + b – c), (a + 3c)x(3a + 4c)|. Найдём

(a + 3c)x(3a + 4c) = 3(a, a) + 4(a, c) +  9(a, c) + 12(c, c) = -5(a, c), так как (a, a) = 0, (c, a) = -(a, c),  (c, c) = 0. Тогда объём параллелепипеда V = |(2a + b – c), (-5)(a x c)| = 5|(2a + b – c), (a x c)| =