Основи теорії захисту інформації: Конспекти лекцій № 1-32 (Введення в криптологію, основні поняття і визначення. Проблеми теорії і практики криптології), страница 29

Лекція № 23 

Оцінка стійкості доказовo стійких криптосистем

1.  Сутність методу Поліга - Хелмана.

2.  Методи оцінки стійкості ймовірно стійких криптосистем.

1. Сутність методу Поліга - Хелмана.

Нехай мається система Діфі - Хелмана чи ЕК:

                                                                                 (1)

Нехай параметри  - доступні КРА.

Тоді аналіз вираження (1) показує, що основним фактором, що визначає складність рішення цього рівняння й одержання секретного ключа:

                                                                                  (2)

порозумівається великою величиною застосовуваного числа

Якщо - первісний елемент, а -простої, то послідовність  для різних значень , буде належати простому полю Галуа. У поле Галуа кожному значенню відповідає своє значення , і навпаки. Тут відкритий ключ і  однозначно зв'язані між собою.

Нам необхідно визначити .

Визначаємо   і                                                  (3)        

Далі знаходимо канонічне розкладання -1:                                                    

                                            (4)

Як правило до числа  пред'являються вимоги, щоб воно було сильне у вузькому чи широкому змісті.

 -1- будемо називати сильним у вузькому змісті якщо воно має вид:

                                                                                                    (5)

Просте число буде вважається сильним у широкому змісті якщо:

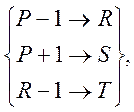                                                                  (6)

де , S, Т – великі прості числа.

Число -1 містить у своєму розкладанні, велике просте число = R.

У заданих умовах необхідно знайти .

Розглянемо можливість рішення задачі на основі застосуванні Китайської теореми про залишки. Теорема затверджує, що:

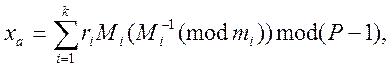                                                                             (7)

де - кількість членів розкладання;

       - залишок числа  по - тім модулі, тобто по модулі ;

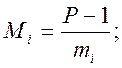                                                                                                 (8)

      - це зворотний елемент ;

     

Число  нам не відомо, тоді як знайти його розкладання?

Очевидно  може бути представлений у виді залишку :

 ;

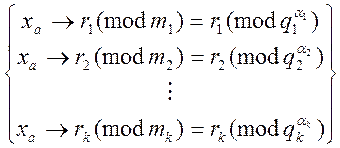Для рішення першим етапом є перебування канонічного розкладання числа -1.

Уявимо собі, що КРА виявляє, що число - сильне у вузькому змісті, тоді йому не треба шукати канонічне розкладання, тому що воно буде дорівнює 2R. У сумі (7) буде 2 суми й операції будуть по модулі 2 і по модулі R. У такий спосіб Китайська теорема нам мало чого дасть.

Розглянемо другий випадок:

Тепер нехай є сильним у широкому змісті. У цьому випадку канонічне розкладання буде більш спектральним, але в ньому все рівно буде міститися велике просте число .

      Розглянемо третій випадок:

Нехай просте число будуватися таким чином, що розроблювачу відомо його розкладання, тобто відомо -1 розкладання, тоді ми можемо побудувати пари . У такий спосіб задача криптоаналізу істотно спрощується. КРА не потрібно вирішувати задачу факторизації -1. У цьому випадку можна сподіватися, що Китайська теорема про залишки може дати якийсь результат.

Нехай у нас залишок  має якесь значення, представимо його у виді - ічного підстави, тоді:

                                                               (9)

;                                                        (10)

                                                                                           (11)

Підносимо до степеня 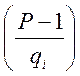 ліву і праву частину, у результаті одержимо:

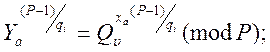                                                                       (12)

Якщо підставити (10) у (12) і після ряду перетворень можна одержати:

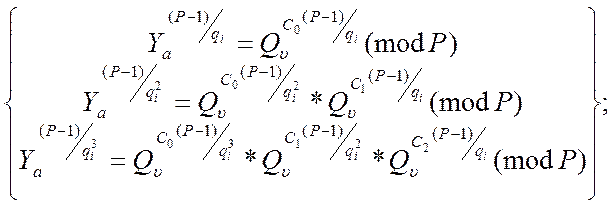                    (13)

Наша задача при відомому  знайти коефіцієнти .

Яким-небудь методом знайдемо  з (13.1)(наприклад підбором), після того як ми знайдемо , підставляємо його в (13.2) і знаходимо  таким же способом. На якомусь кроці ми знайдемо всі коефіцієнти .

     У такий же спосіб необхідно визначити коефіцієнти всіх залишків  . Далі підставляємо отримані значення   у вираження (7). У такий спосіб ми можемо знайти  ключ.