Итак, принцип поляризационной
двойственности дает возможность представить решение уравнений Максвелла в виде
суммы фундаментальных решений ТМ и ТЕ типа относительно координаты разделения ![]() . Каждое из решений описывается
однокомпонентным вектором Герца
. Каждое из решений описывается
однокомпонентным вектором Герца ![]() , для которого
справедливо уравнение (1.65). В ряде случаев оно может быть сведено к уравнению
Гельмгольца. Отметим, что вывод формул (1.66) и (1.67) основан на условиях (1.57).
Если в выбранной координатной системе эти условия не выполняются, то данный
способ решения оказывается неприменимым. В такой координатной системе общее
решение уравнений поля не распадается на сумму решений электрического и
магнитного типов.
, для которого
справедливо уравнение (1.65). В ряде случаев оно может быть сведено к уравнению
Гельмгольца. Отметим, что вывод формул (1.66) и (1.67) основан на условиях (1.57).
Если в выбранной координатной системе эти условия не выполняются, то данный
способ решения оказывается неприменимым. В такой координатной системе общее
решение уравнений поля не распадается на сумму решений электрического и
магнитного типов.
Рассмотрим несколько простейших координатных систем, удовлетворяющих условиям (1.57), и запишем выражения для компонент ЭМП.
Декартовая система координат (СК) (x, y, z):
Параметры Ламэ ![]() . Оба условия (1.57)
выполняются, любая из координат может быть координатой разделения. Пусть
. Оба условия (1.57)
выполняются, любая из координат может быть координатой разделения. Пусть ![]() .
.
Уравнение (1.65) принимает вид
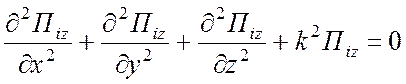 (1.68)
(1.68)
и совпадает с уравнением Гельмгольца.
Компоненты электромагнитного поля:
ТМ типа относительно z -
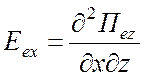 ,
, 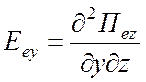 ,
, 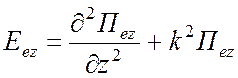 ,
,
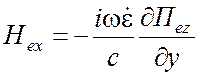 ,
,
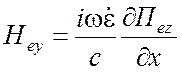 ,
, ![]() ; (1.69)
; (1.69)
ТЕ типа относительно z -
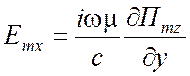 ,
, 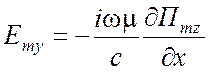 ,
, ![]() ,
,
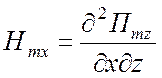 ,
,
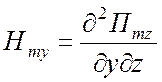 ,
, 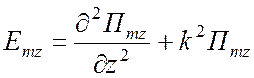 . (1.70)
. (1.70)
В цилиндрической системе координат ![]() :
:
![]() ,
, ![]() .
.
Условия (1.57) выполняются, если за координату разделения взять z.
Уравнение для вектора Герца также совпадает с уравнением Гельмгольца
![]() (см. формулу (П1.14) Приложения
1), а для компонент ЭМП получаем выражения:
(см. формулу (П1.14) Приложения
1), а для компонент ЭМП получаем выражения:
для ТМ типа относительно координаты разделения z -
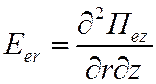 ,
, 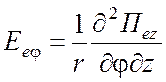 ,
, 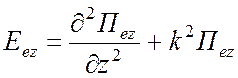 ,
,
 ,
,
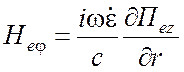 ,
, ![]() ;
(1.71)
;
(1.71)
для ТЕ типа относительно координаты разделения z -
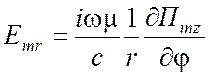 ,
, 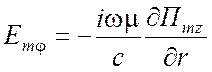 ,
, ![]() ,
,
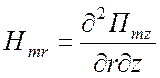 ,
,
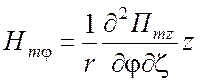 ,
, 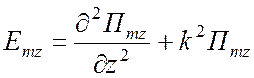 .
(1.72)
.
(1.72)
С помощью комплексных уравнений
поля исследуем распространение монохроматических плоских электромагнитных волн
в однородной безграничной среде с постоянными комплексными проницаемостями ![]() и
и ![]() . Плоской
электромагнитной волной называется электромагнитное поле, векторы которого в
каждый момент времени принимают постоянные значения на системе параллельных
плоскостей. Таким образом, если выбрать ось z перпендикулярной этим плоскостям, то в монохроматической
плоской волне комплексные амплитуды полей
. Плоской
электромагнитной волной называется электромагнитное поле, векторы которого в
каждый момент времени принимают постоянные значения на системе параллельных
плоскостей. Таким образом, если выбрать ось z перпендикулярной этим плоскостям, то в монохроматической
плоской волне комплексные амплитуды полей ![]() и
и
![]() будут зависеть только от координаты z, но не от координат х и у.
будут зависеть только от координаты z, но не от координат х и у.
Запишем однородные векторные уравнения Максвелла (1.17), (1.37) в декартовой системе координат х, у, z:
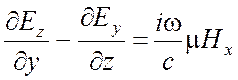 ,
, 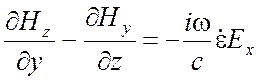
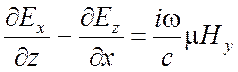 ,
, 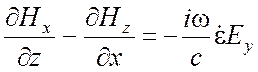
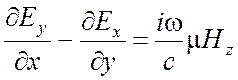 ,
,
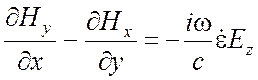 (2.1)
(2.1)
Для плоской волны производные по х и у равны нулю и уравнения (2.1) значительно упрощаются. Прежде всего, из третьего уравнения каждого столбца получаем
![]() ,
,
![]() ,
(2.2)
,
(2.2)
откуда видно, что плоские электромагнитные волны в любой среде суть волны поперечные.
Комбинируя затем попарно
уравнения, в которые входят Ех и Ну, с
одной стороны, и Еу и Нх, с другой стороны,
приходим к двум независимым системам уравнений (в которых символ частной
производной ![]() заменен на d/dz, поскольку все величины зависят только от z):
заменен на d/dz, поскольку все величины зависят только от z):
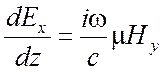 ,
, 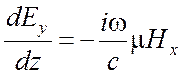
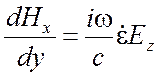 ,
,
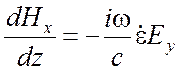 .
(2.3)
.
(2.3)
Исключая из каждой системы какую-нибудь одну функцию, для каждой из четырех величин Еx, Ну, Еу и Нх получаем простое уравнение
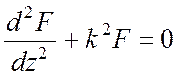 ,
(2.4)
,
(2.4)
где 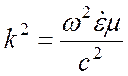 - комплексное волновое
число в среде. Дифференциальное уравнение (2.4) имеет общее решение
- комплексное волновое
число в среде. Дифференциальное уравнение (2.4) имеет общее решение
![]() ,
(2.5)
,
(2.5)
где C1, C2 – произвольные постоянные. Написав для четырех величин Ех, Ну, Еу и Нх выражения такого вида с разными постоянными и подставив их в уравнения (2.3), приходим окончательно к следующим выражениям:
![]() ,
, ![]() ,
,
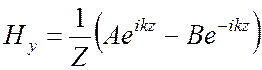 ,
,
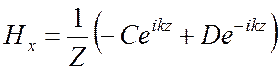 , (2.6)
, (2.6)
где 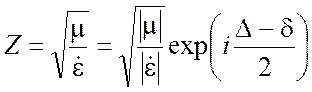 - комплексный волновой
импеданс данной среды, смысл которого поясним позже.
- комплексный волновой
импеданс данной среды, смысл которого поясним позже.
Разберем физический смысл выражений для Ех и Ну, причем ограничимся только первым слагаемым, положив в (2.6) B = 0:
![]() ,
,
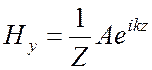 (2.7)
(2.7)
Перейдем к физическим величинам, полагая
![]() ,
, ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.