Основные положения теории электромагнитного поля. Плоские электромагнитные волны. Волны в регулярном волноводе. Потери в волноводах. Возбуждение электромагнитных волн, страница 19

При изложении теории волноводов предполагалось, что стен­ки волноводов обладают идеальной проводимостью. Разумеется, в реальных условиях проводимость стенок всегда конечна. Конечная проводимость стенок может быть учтена с помощью приближен­ных граничных условий Леонтовича, применимых при сильном скин-эффекте. Так как волноводы обычно исполь­зуются в сантиметровом диапазоне, где толщина скин - слоя имеет порядок микрона или даже меньше, то скин-эффект в металлических стенках волновода является сильным и можно за­писать на поверхности стенок граничное условие (4.8). Заметим, что волновой импеданс Z  металлов есть безразмерное комплексное число, имеющее весьма малую абсолютную величину. Если положить Z = 0, то граничное условие (4.8) принимает вид (1.33)  = 0, т.е. переходит в граничное условие E_t = 0 для идеально прово­дящих стенок. Малость параметра Z означает, что структура электромагнитного поля волны в волно­воде с металлическими стенками мало отличается от структуры поля в волноводе, стенкам которого приписывается идеальная про­водимость.

Итак, рассмотрим задачу о волноводе со стенками, обладающими большой, но конечной проводимостью, и определим коэффициент затухания. Считаем, что волновод регулярный, заполнение – пустота. Обозначим комплексные диэлектрическую и магнитную проницаемости среды стенок волновода индексом 2 и введем коэффициент, имеющий смысл относительного волнового сопротивления

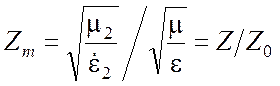,                                       (4.10)

где Z – волновое сопротивление стенок волновода, Z₀ - волновое сопротивление вакуума. Считаем Z_m малой величиной Z_m << 1. Тогда, приближенное граничное условие Леонтовича на границе раздела, совпадающей с некоторым контуром С, запишется в виде

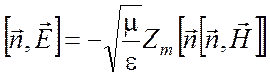                                       (4.11)

Воспользуемся формулами для компонент электрического и магнитного полей в регулярном волноводе (см. § 3.1), выраженными через электрическую (3.9) и магнитную (3.15) мембранные функции

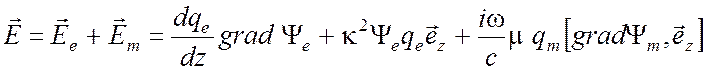,       (4.12)

,

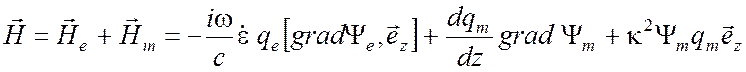где мембранные функции удовлетворяют уравнениям (3.7):

.                                       (4.13)

Подставим эти выражения в условие (4.11). Введем единичные вектора , направленные соответственно нормально и касательно к стенкам волновода, тогда векторное условие (4.12) сведется к двум скалярным

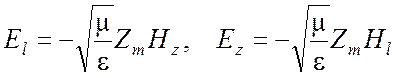.                          (4.14)

После подстановки в них выражений (4.12), приходим к системе двух уравнений связывающих электрическую и магнитную мембранную функцию

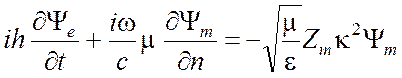 на С,                    (4.15а)

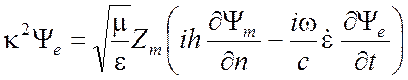 на С.                   (4.15б)

Таким образом, имеем две граничные задачи для функций  и , удовлетворяющих уравнениям (4.13) и граничным условиям (4.15). Для построения решения воспользуемся малостью параметра Z_m и применим метод возмущений. В качестве невозмущенной задачи возьмем решение для волновода с идеальными стенками. Тогда, при стремлении Z_m 0 из условий (4.15) приходим к идеальным граничным условиям (3.11) и (3.17)

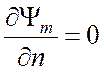 на С и  на С.

Ищем общее решение задачи  в следующем виде:

,                                      (4.16)

,  ,

где индексом (0) обозначено решение невозмущенной задачи при Z_m 0.

Подставив выражения (4.16) в уравнения (3.13) и граничные условия (4.15) и удерживая лишь слагаемые первого порядка малости включительно, получаем следующие выражения:

,                                        (4.17)

,                          (4.18)

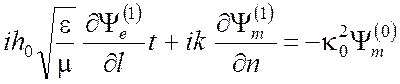 на С,                           (4.19)

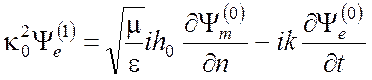 на С.                            (4.20)

Заметим, что в этих формулах учтены также условия (3.11), (3.17) для нулевого приближения.

Преобразуем эти соотношения и найдем выражение для . Для этого умножим уравнение (4.17) на , а уравнение (4.18) - на  и вычтем из первого уравнения второе. Воспользовавшись некоторыми формулами векторного анализа и теоремой Гаусса – Остроградского (см. (П1.21) Приложения 1) для двумерного случая, получаем искомое выражение в виде

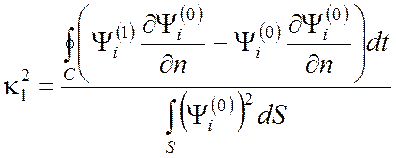                            (4.21)

Рассмотрим случай электрического поля, для которого выполняется  на С, и учтем также условие (4.19). В результате для поперечно магнитного ТМ поля получаем: