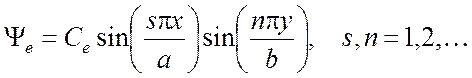Основные положения теории электромагнитного поля. Плоские электромагнитные волны. Волны в регулярном волноводе. Потери в волноводах. Возбуждение электромагнитных волн, страница 10

                     (3.25)

где С_е — произвольная постоянная. Собственная функция  (3.25) соответствует по формулам   (3.21)  и  (3.24)  собственному значению

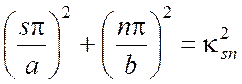,                                           (3.26)

Заметим, что ни одно из чисел s или п нельзя брать равным нулю, так как это приводит к функции (3.25), тождественно рав­ной нулю. Если же взять в качестве s или п отрицательное целое число, то нового решения не получим, так как это приведет лишь к изменению знака постоянной С_е в формуле (3.25).

Собственные функции (3.25) и собственные значения (3.26) исчерпывают все возможные решения граничной задачи. Собственная функция (3.25) и собственное значение (3.26) определяют электрическую волну, которая называется волной Е_sп в прямоугольном волноводе.

Граничная задача для магнитных волн решается аналогичным образом: ищем функцию , которая должна удовлетворять двумерному волновому уравнению (3.7) в виде произведения (3.18). Рассуждая таким же образом, как и выше, получаем для функций X_m и Y_m  уравнения  (3.20) и  общие решения (3.22). Функция  в этом случае должна удовлетворять граничным условиям (3.17).

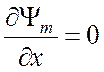 при х = 0 и х = а, 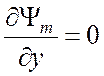 при у = 0 и у = b,                 (3.27)

поэтому

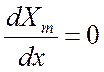при х = 0, откуда А_2m = 0;

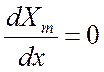при   х = а,  откуда;

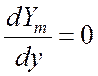при   y = 0, откуда  B_2m = 0;

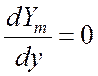при   y = b, откуда  .

Таким образом, для получения нетривиального решения гранич­ной задачи необходимо выбрать числа и , удовлетворяющие тем же самым уравнениям, которые были получены выше для электрических волн. Поэтому возможные значения и  по-прежнему определяются формулами (3.24) с тем лишь отли­чием, что индексы s и п могут быть также равными нулю. Дейст­вительно, при s = 0  имеем  Х_m = А_1m  и функция  в нуль не обращается.

Окончательно получаем собственные функции

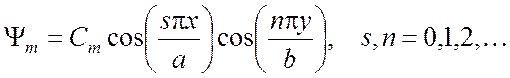                  (3.28)

и собственные значения

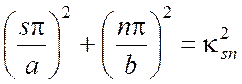.(3.29)

Они определяют магнитную волну, которая называется волной Н_sп в прямоугольном волноводе.

Заметим, что среди магнитных волн в волноводе имеются вол­ны Н₁₀, Н₂₀, ..., Н₀₁, Н₀₂,..., однако волна Н₀₀, у которой оба ин­декса равны нулю и , отсутствует, так как по формулам (3.15), (3.16) такой волне соответствовало бы электромагнитное поле, равное тождественно нулю. Отметим также, что поле волны Н₁₀ (а также волн Н₂₀, ...) не зависит от координаты у. Подоб­ная ей волна  Е₁₀ не может существовать по следующей причине: поле такой волны не должно зависеть от координаты у, но так как при у = 0 и у = b должно быть E_z = 0, то вследствие независимости E_z от у составляющая E_z должна тождественно обращаться в нуль. А это означает, что такой волны нет.

Рассмотрим структуру электромагнитных полей. Простейшая электрическая волна в прямоугольном волноводе есть волна Е₁₁, у которой

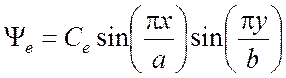.                                (3.30)

Построим картину силовых линий.  Можно показать, что такие линии совпадают с линиями уровня функции  = const. Действительно, для поперечно магнитного ТМ(Е) поля имеются только две компоненты магнитного поля, отличные от нуля и в этом случае уравнение силовых линий есть , где  - касательный орт. Подставив выражение для магнитного поля (3.10), получим двойное векторное произведение и, преобразовав его, получим

,

или

.

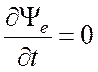Нанеся линии уровня  = const, путем построения семейства кривых, им ортогональных, получим картину электрических сило­вых линий в плоскости поперечного сечения. Точнее, это проекции электрических силовых линий, являющихся трехмерными пространственными кривыми, на плоскость поперечного сечения. Из формул (3.9),  (3.10) вытекает соотношение

,             (3.31)

Каждое из компонент равно нулю по формулам для смешанного произведения, поэтому электрическое поле в каждой точке перпендикулярно маг­нитному и магнитные силовые линии совпадают с линиями уровня функции (х, у). Так как H_z = 0, то магнитные силовые линии являются плоскими кривыми.