Основные положения теории электромагнитного поля. Плоские электромагнитные волны. Волны в регулярном волноводе. Потери в волноводах. Возбуждение электромагнитных волн, страница 27

Как известно, плотность сторонних электрических токов характеризуется объемной плотностью дипольного момента , причем справедливо

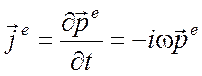.                                          (6.9)

Очевидно, что плотность тока , соот­ветствующая элементарному диполю, равна нулю всю­ду, за исключением точки, где расположен диполь. В этой точке плотность тока  бесконечна, причем интеграл по объему V , внутри которого находится эта точка, имеет конечное значение

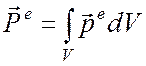
Пусть теперь поле  возбуждено диполем  находящимся в точке 1, а поле  - диполем , расположенным в точке 2. Применим к этим полям лемму Лоренца в простейшей форме (6.8). Так как функции  и  обращаются в нуль всюду, за исключением точек 1 и 2 соответственно, то

,

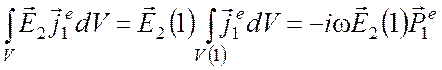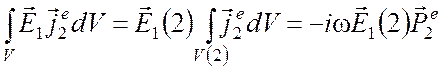
откуда

,                                   (6.10)

где через   обозначено значение электрического поля  в точке 1, где расположен диполь , а  есть значение поля  в точке 2, где находится второй диполь .

Если воспользоваться трехмерными дельта - функциями, то плотнос­ти тока, соответствующие элементарным диполям  и , можно записать в виде

,                      (6.11)

где  и  - радиус - векторы точек 1 и 2 соответственно,  - текущий радиус - вектор с компонентами х, у, z. Пользуясь форму­лой (6.8) и известным свойством дельта - функций, снова приходим к формуле (6.10).

Соотношение (6.10) есть теорема взаимности для элементар­ных электрических диполей. Если взять для простоты моменты  и  по абсолютной величине равными единице, то левая часть соотношения (6.10) будет равна электрическому полю диполя , действующему на диполь , а правая часть - электрическому полю диполя , действующему на диполь . При этом называем, например, проекцию вектора  на направление вектора  полем, действующим на этот диполь, так как именно эта состав­ляющая поля воздействует на диполь  возбуждая ток в соот­ветствующем отрезке проводника 1. Поэтому теорему взаимности (6.10) можно сформулировать более кратко следующим образом: при равенстве абсолютных величин дипольных моментов, дейст­вие диполя 2 на диполь 1 равно действию диполя 1 на диполь 2.

Приведем простой пример применения доказанной теоремы взаимности. Пусть диполь  расположен в точке 1 вблизи земли (рис. 6.1), и нужно найти создаваемое им поле на большой высоте в точке 2, в которой находится приемная антенна самолетной ра­диоустановки. Полное вычисление электромагнитного поля антенны, расположенной у земной поверхности, является довольно слож­ной задачей. Однако требуемое поле в точке 2 легко найти, не решая этой задачи. А именно, поставим в точке 2 вспомогательный излучающий диполь ; так как он находится на большом расстоя­нии от точки 1, то излучаемую им сферическую волну можно в окрестности точки 1 считать плоской, а электромагнитное поле, возникающее при падении плоской волны на плоскую границу раздела двух сред, хорошо известно. По из­вестному полю  легко определяется с помощью теоремы вза­имности (6.10) искомое поле .

В связи с этим примером можно сказать, что в интересующей нас задаче в точке 1 находится передающая антенна, а в точке 2 - приемная. Вместо этого решается вспомогательная задача, в которой в точке 2 расположена передающая антенна, а в точке 1 - приемная, и применяется соотношение (6.10). С помощью леммы Лоренца можно обобщить теорему взаимности таким об­разом, чтобы она относилась не только к идеализированным антеннам - элементарным диполям, но и к реальным ан­теннам и антенным системам.

Заметим также, что теоремы взаимности в общих случаях связы­вают свойства данной приемной антенны со свойствами той же антенны при работе на передачу. В частности, оказывается, что диаграммы направленности любой антенны при работе на прием и на передачу совпадают.

Обобщим соотношения (6.10) на случай, когда поля  и  создаются не электрическими, а магнитными диполями, расположенными в точках 1 и 2 и имеющими моменты  и  соответственно. Магнитный диполь формально определяется с по­мощью магнитного тока, плотность которого  равна нулю всюду, за исключением одной точки. Интеграл по окрестности V₀ этой точки связан с моментом магнитного диполя  соотношением