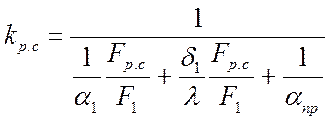Теория теплообмена. Теплопроводность. Основные положения теории теплопроводности. Теплопроводность при стационарном режиме. Теплопроводность при нестационарном режиме. Теплообмен при фазовых превращениях, страница 18

        , Вт/(м²·K) – коэффициент теплопередачи через ребристую стенку при отнесении теплового потока к оребренной поверхности.

Если Q отнести к неоребренной поверхности стенки F₁, то:

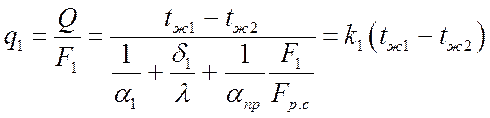                        , Вт/м²,

где 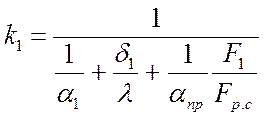  , Вт/(м²·K) – коэффициент иеплопередачи при отнесении теплового потока к гладкой неоребренной поверхности.

Отношение 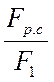 называется коэффициентом оребрения. При отсутствии оребрения коэффициент оребрения равен 1, т. к. .

Влияние оребрения проследим на примере. Пусть a₁ = 1000 Вт/(м²·K), a₂ = 20 Вт/(м²·K). Положим, что  мало, и им можно пренебречь, тогда:

                                            Вт/(м²·K).

Если стенка имеет ребра с одной стороны, причем коэффициент оребрения 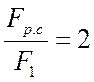, то:

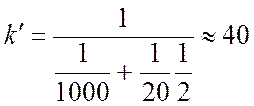                                           Вт/(м²·K).

Таким образом, при заданных соотношениях коэффициента теплоотдачи при оребрении плоской стенки со стороны малого a с коэффициентом оребрения, равным 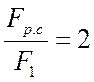, то передача тепла увеличивается приблизительно в два раза.

3.8. Теплопроводность круглого ребра

Рассмотрим расчет теплопроводности круглого ребра постоянной толщины. Круглые ребра применяются при оребрении цилиндрических поверхностей (труб).

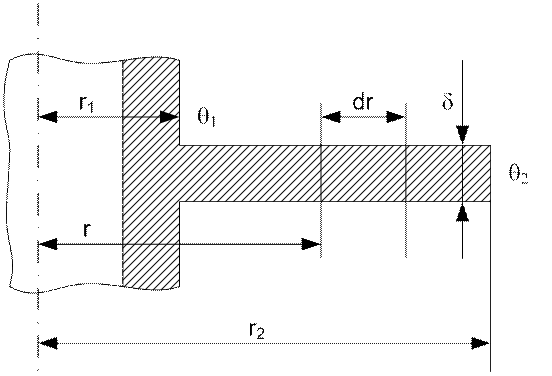
Рис. 25. Теплопроводность круглого ребра

Задано: внутренний радиус ребра r₁, наружный радиус ребра r₂, толщина d, коэффициент теплопроводности l.

Температура окружающей среды . Избыточная температура ребра будет:

                                                            .

Коэффициент теплоотдачи по поверхности ребра a, температура у основания ребра q₁. Режим стационарный, и температура изменяется только вдоль ребра по радиусу.

Уравнение баланса энергии для кольцевого элемента ребра толщиной dr:

                                                        .

Дифференциальное уравнение после нахождения составляющих:

                                                  .

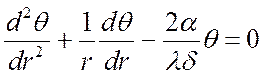Обозначим:

                   , , , , , .

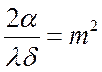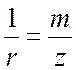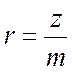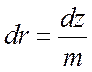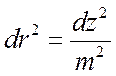Подставим:

                                              , .

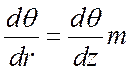Тогда дифференциальное уравнение примет вид:

                                                    .

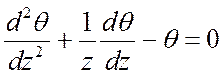Это уравнение представляет собой уравнение Бесселя, имеющее общее решение в виде:

                                                  ,

где    – модифицированная функция Бесселя первого рода нулевого порядка мнимого аргумента;

         – модифицированная функция Бесселя второго рода нулевого порядка мнимого аргумента.

Свойства этих функций:

      при  , , , ,

   при   и , , .

Постоянные интегрирования C₁ и C₂ определяются из граничных условий.

Если пренебречь теплоотдачей с торца ребра, то будем иметь следующие расчетные формулы:

для текущей температуры в ребре:

                                   ,

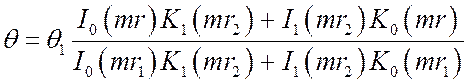для температуры на конце ребра:

                                  ,

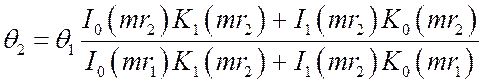для количества тепла:

                                       ,

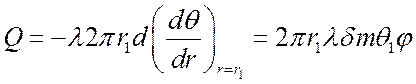где   .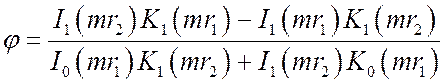

Приведенные уравнения неудобны для технических расчетов, т. к. достаточно сложны. Поэтому решение задачи можно упростить, сведя расчет к методике расчета прямых ребер постоянного сечения.

Количество тепла, отдаваемое поверхностью круглого ребра:

                                                        , Вт,                     (*)

где   Q¢ – тепло, отдаваемое круглым ребром;

        F¢ – поверхность круглого ребра;

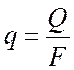         – количество тепла, отдаваемое в единицу времени единицей поверхности прямого ребра, толщина которого равна толщине круглого, а длина равна 1 м;

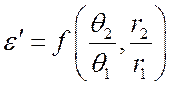         – поправочный коэффициент, определяемый по таблицам и графикам;

         – отношение температур на концах ребра, вычисленных по формулам для прямого ребра постоянного сечения.

Таким образом, вычислив температуру на конце ребра и плотность теплового потока для прямого ребра и подставив q и e¢ в уравнение (*), получим значение теплового потока для круглого ребра.

3.9. Теплопроводность при наличии внутренних источников тепла