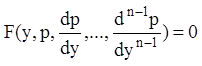 .
(7.43)
.
(7.43)
Если бы мы сумели проинтегрировать его, то имели бы:
![]() (7.44)
(7.44)
или:
![]() .
(7.45)
.
(7.45)
Если уравнение (7.45) интегрируется в квадратурах, то задача была бы решена до конца.
П р и м е р 5. Решить
уравнение ![]() .
.
Р е ш е н и е. Это уравнение вида (7.42). Замена
![]() или
или
![]() , т.е.
, т.е.
![]() . Тогда
. Тогда ![]() .
.
Используя начальные условия,
находим ![]() :
: ![]() .
Тогда
.
Тогда ![]() . Это уравнение с разделяющимися
переменными:
. Это уравнение с разделяющимися
переменными:
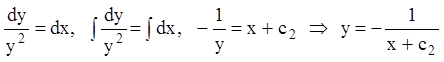 .
.
Находим ![]() из начальных условий:
из начальных условий: 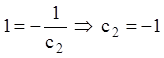 . Тогда частное решение запишется
. Тогда частное решение запишется 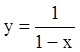 .
.
3) Уравнение (7.37) однородное относительно искомой функции и ее производных. По условию левая часть уравнения (7.37) удовлетворяет тождеству:
![]() ,
,
где m – показатель однородности. Тогда уравнение (7.37) можно записать в виде:
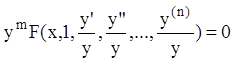 .
(7.46)
.
(7.46)
Замена
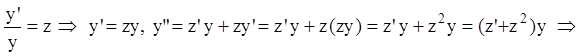
![]() и
т.д.
и
т.д.
Подставляя в (7.46), получаем уравнение (n-1)-го порядка:
![]() .
(7.47)
.
(7.47)
Если в (7.47) не входит явно x, то его порядок можно понизить еще на единицу.
П р и м е р 6. Решить
уравнение ![]() .
.
Р е ш е н и е. Это однородная
функция относительно y,y' и y". Замена: 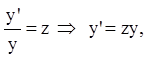
![]() и
и 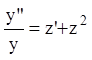 .
Подставляем в уравнение
.
Подставляем в уравнение ![]() (т.к.
(т.к. ![]() ),
), ![]() или
или 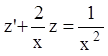 - это линейное дифференциальное уравнение
первого порядка. Его общее решение имеет вид:
- это линейное дифференциальное уравнение
первого порядка. Его общее решение имеет вид: 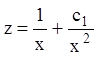 .
Учитывая, что
.
Учитывая, что 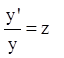 , получаем
, получаем 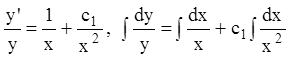 ,
, 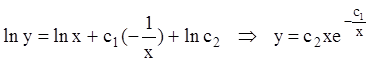 - общее
решение.
- общее
решение.
4) Порядок уравнения понижается, если оно является
однородным относительно x и y в обобщенном смысле, т.е. не меняется от замены ![]() на
на ![]() ,
, ![]() на
на ![]() (при этом
(при этом ![]() заменяется на
заменяется на ![]() ,
, ![]() и т.д.,
и т.д., ![]() ).
Чтобы узнать, будет ли уравнение однородным и найти число m,
надо приравнять друг к другу показатели степеней, в которых число k
будет входить в каждый член уравнения после указанной выше замены в одинаковых
степенях. Например,
).
Чтобы узнать, будет ли уравнение однородным и найти число m,
надо приравнять друг к другу показатели степеней, в которых число k
будет входить в каждый член уравнения после указанной выше замены в одинаковых
степенях. Например, ![]() . Замена:
. Замена: ![]() . Получаем
. Получаем ![]() .
Чтобы уравнение было однородным, необходимо выполнение равенств
.
Чтобы уравнение было однородным, необходимо выполнение равенств ![]() (Если же полученные уравнения будут
несовместными, то рассматриваемое дифференциальное уравнение не является
однородным в указанном смысле).
(Если же полученные уравнения будут
несовместными, то рассматриваемое дифференциальное уравнение не является
однородным в указанном смысле).
Для интегрирования уравнения проводим замену:
![]() , где
, где ![]() . (7.48)
. (7.48)
Тогда:
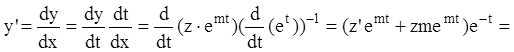
![]() .
.
Аналогично:
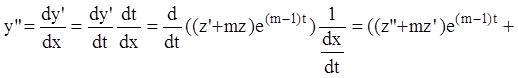
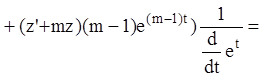
![]() и
т.д.
и
т.д. ![]() .
.
После проведения замены исходное уравнение не содержит независимой переменной t и поэтому допускает понижение порядка на единицу.
П р и м е р . Решить
уравнение ![]() .
.
Р е ш е н и е. Установим,
является ли это уравнение обобщенным однородным уравнением, заменяя ![]() , получим:
, получим: ![]() ,
отсюда:
,
отсюда: ![]() . Замена:
. Замена: ![]() .
Отсюда:
.
Отсюда: ![]() . Тогда
. Тогда ![]() .
Сократив на
.
Сократив на ![]() , получаем
, получаем ![]()
![]() . Отсюда:
. Отсюда: ![]() . Это
уравнение явным образом не содержит независимую переменную, поэтому замена:
. Это
уравнение явным образом не содержит независимую переменную, поэтому замена: ![]() . Тогда:
. Тогда: ![]() .
Замена:
.
Замена: 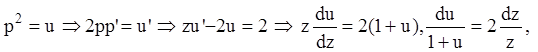
![]() ,
,![]()
![]() . Вычислив интеграл,
получим
. Вычислив интеграл,
получим ![]() . Учитывая, что
. Учитывая, что ![]() ,
получаем:
,
получаем:
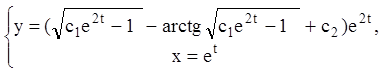
Исключив параметр t, получаем общее решение:
![]() .
.
5) Уравнения в точных производных. Левая часть уравнения:
![]() (7.49)
(7.49)
является производной некоторого
дифференциального выражения (n-1)-го порядка 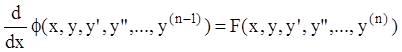 .
Тогда заданное уравнение можно переписать в виде
.
Тогда заданное уравнение можно переписать в виде 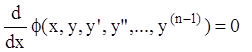 ,
тогда:
,
тогда: ![]() . Таким образом, порядок уравнения
понизился на единицу.
. Таким образом, порядок уравнения
понизился на единицу.
П р и м е р 7. Решить
уравнение ![]() .
.
Р е ш е н и е. Это уравнение
вида 5), т.к. его можно записать в виде ![]() или
или ![]() . После интегрирования получаем
. После интегрирования получаем 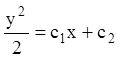 - общий интеграл.
- общий интеграл.
Если исходное уравнение
(7.49) не является уравнением в точных производных, то иногда удается подобрать
такую функцию ![]() (интегрирующий множитель), что
после умножения на нее уравнение (7.49) становится уравнением в точных
производных. При умножении на
(интегрирующий множитель), что
после умножения на нее уравнение (7.49) становится уравнением в точных
производных. При умножении на ![]() могут быть введены
лишние решения (решения уравнения
могут быть введены
лишние решения (решения уравнения ![]() ), а также возможна
потеря решений (в случае разрывности множителя
), а также возможна
потеря решений (в случае разрывности множителя ![]() ).
).
П р и м е р 8. Решить
уравнение ![]() .
.
Р е ш е н и е. Умножая
уравнение на множитель 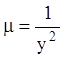 , получаем:
, получаем:
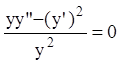 или
или 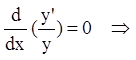
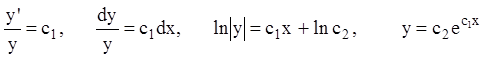 .
.
З а м е ч а н и е 1. Линейное уравнение второго порядка
![]()
будет уравнением в точных производных
тогда, и только тогда, когда ![]() , т.е. если оно имеет
вид:
, т.е. если оно имеет
вид:
![]() .
.
Тогда его можно представить в виде:
![]() .
.
Откуда ![]() - линейное дифференциальное уравнение
первого порядка. Отсюда:
- линейное дифференциальное уравнение
первого порядка. Отсюда:
![]() .
.
П р и м е р. Решить
уравнение 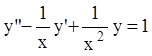 .
.
Р е ш е н и е.
Т.к.
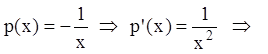
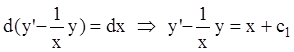 .
.
Решив линейное уравнение, получим общее решение:
![]() .
.
З а м е ч а н и е 2. Уравнение вида
![]()
умножаем на ![]() , получаем
, получаем
![]()
![]() ;
;
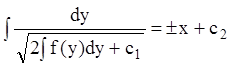 -
общий интеграл.
-
общий интеграл.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.