П р и м е р 4. Имеет ли уравнение 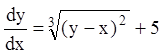 особое
решение?
особое
решение?
Р е ш е н и е. Правая часть этого уравнения непрерывна, но
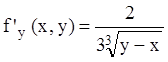 неограниченно возрастает при приближении
к прямой
неограниченно возрастает при приближении
к прямой ![]() . Следовательно, на прямой
. Следовательно, на прямой ![]() может нарушаться единственность. Но
функция
может нарушаться единственность. Но
функция ![]() не удовлетворяет заданному уравнению,
следовательно, особого решения нет.
не удовлетворяет заданному уравнению,
следовательно, особого решения нет.
П р и м е р 5. Имеет ли уравнение 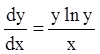 особое
решение?
особое
решение?
Р е ш е н и е. В данном уравнении 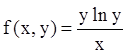 -
непрерывная функция в любой замкнутой области, где
-
непрерывная функция в любой замкнутой области, где ![]() ( при
( при ![]() можно положить, что
можно положить, что 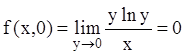 ).
). 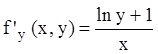 ,
откуда следует, что
,
откуда следует, что ![]() .
.
Следовательно, геометрическое место точек ![]() может быть особым решением уравнения.
Очевидно, что
может быть особым решением уравнения.
Очевидно, что ![]() есть решение исходного уравнения.
Проверим, нарушается ли свойство единственности (п.3) в каждой точке решения
есть решение исходного уравнения.
Проверим, нарушается ли свойство единственности (п.3) в каждой точке решения ![]() . Для этого находим общее решение:
. Для этого находим общее решение:
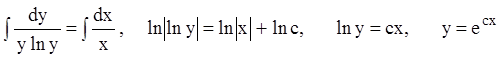 .
.
Решение ![]() может быть получено из
общего решения при
может быть получено из
общего решения при ![]() . Поэтому через каждую точку оси
OY (кроме точки
. Поэтому через каждую точку оси
OY (кроме точки ![]() )
проходит лишь одна интегральная прямая
)
проходит лишь одна интегральная прямая ![]() .
Значит, особых решений уравнение не имеет.
.
Значит, особых решений уравнение не имеет.
Рассмотрим вопрос о существовании особых решений дифференциальных уравнений, не разрешенных относительно производной
![]() .
(6.37)
.
(6.37)
Если функция![]() в некоторой области
в некоторой области ![]() трехмерного пространства удовлетворяет
условиям теоремы существования неявной функции, то в соответствующей плоскости
через каждую точку
трехмерного пространства удовлетворяет
условиям теоремы существования неявной функции, то в соответствующей плоскости
через каждую точку ![]() по данному направлению проходит
лишь одна интегральная кривая уравнения (6.37). Следовательно, особые решения
уравнения (6.37) могут проходить лишь через те точки, в которых нарушается
условие вышеуказанной теоремы.
по данному направлению проходит
лишь одна интегральная кривая уравнения (6.37). Следовательно, особые решения
уравнения (6.37) могут проходить лишь через те точки, в которых нарушается
условие вышеуказанной теоремы.
В частности, если ![]() непрерывна
и имеет непрерывные частные производные первого порядка, то особые решения
следует искать среди тех точек, координаты которых одновременно удовлетворяют
уравнениям:
непрерывна
и имеет непрерывные частные производные первого порядка, то особые решения
следует искать среди тех точек, координаты которых одновременно удовлетворяют
уравнениям:
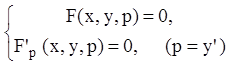 .
(6.38)
.
(6.38)
Если уравнения (6.38) совместны, т.е. существует значение
![]() , удовлетворяющее сразу двум уравнениям из
(6.38), то, исключая из них параметр р, мы получим в общем случае некоторое
геометрическое место точек
, удовлетворяющее сразу двум уравнениям из
(6.38), то, исключая из них параметр р, мы получим в общем случае некоторое
геометрическое место точек ![]() , которое может быть
особым решением уравнения (6.37).
, которое может быть
особым решением уравнения (6.37).
Геометрическое место точек ![]() ,
получаемых путем исключения параметра р из системы уравнений (6.38), называется
р-дискриминантной кривой уравнения (6.37) (РДК).
,
получаемых путем исключения параметра р из системы уравнений (6.38), называется
р-дискриминантной кривой уравнения (6.37) (РДК).
Таким образом, р-дискриминантные кривые уравнения (6.37), если они существуют, могут быть особыми решениями данного уравнения.
Отсюда вытекает один из способов нахождения особых решений уравнения (6.37). Для этого нужно:
найти его р-дискриминантные кривые, исключив параметр р из системы (6.38);
проверить, являются ли р-дискриминантные кривые интегральными кривыми данного уравнения;
проверить, нарушается ли свойство единственности в точках этих интегральных кривых.
Если пункты 1)-3) выполняются, то полученные таким образом решения уравнения (6.37) есть особые.
П р и м е р 6. Имеет ли уравнение особые решения
![]() .
(6.39)
.
(6.39)
Р е ш е н и е. Составляем уравнения для р-дискриминантной кривой:
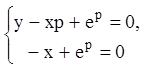 .
.
Исключаем параметр р : ![]() (6.40)
– р-дискриминантная кривая уравнения (6.39). Непосредственной подстановкой
убеждаемся, что (6.40) есть решение уравнения (6.39).
(6.40)
– р-дискриминантная кривая уравнения (6.39). Непосредственной подстановкой
убеждаемся, что (6.40) есть решение уравнения (6.39).
Так как уравнение (6.39) есть уравнение Клеро, то его общим решением является семейство прямых
![]() . (6.41)
. (6.41)
Тогда видим (рис.23), что через каждую точку интегральной кривой (6.40) проходят две интегральные кривые: сама кривая (6.40) и прямая из семейства (6.41), имеющие одинаковые направления. Поэтому решение (6.40) есть особое решение уравнения (6.39).
Кроме изложенного выше способа нахождения особого решения дифференциального уравнения (6.37), существует другой способ, в основе которого лежит понятие огибающей однопараметрического семейства кривых.
Пусть имеем однопараметрическое семейство кривых:
![]() ,
(6.42)
,
(6.42)
где с- параметр, изменяющийся на отрезке ![]() . Кривая l
называется огибающей семейства кривых (6.42), если она в каждой своей точке
имеет касательную, общую с одной из кривых заданного семейства (6.42)
(рис.25).
. Кривая l
называется огибающей семейства кривых (6.42), если она в каждой своей точке
имеет касательную, общую с одной из кривых заданного семейства (6.42)
(рис.25).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.