Дифференциальные уравнения и математическое моделирование. Основные понятия дифференциальных уравнений. Метод Изоклин, страница 11

Линейное уравнение остается линейным при таких преобразованиях:

1) замена независимой переменной , , где  - произвольная дифференцируемая функция, причём,  в рассматриваемом интервале изменения ;

2) замена искомой функции  на , где  и  - любые известные дифференцируемые функции, причём, , а  - искомая функция.

Действительно, в первом случае 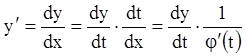, и уравнение (3.1) запишется:

 

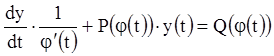
или

,

т. е. уравнение снова остается линейным.

Во втором случае, положив , получаем 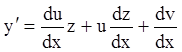. Подставляем в (3.1)

 , или

, или

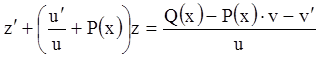 - линейное уравнение.

Свойства решений линейного уравнения:

1. Если известно какое-то частное решение  линейного однородного уравнения (3.2), то его общее решение будет , где  - произвольная постоянная. Функция  удовлетворяет уравнению и имеет произвольную постоянную.

2. Если известно одно частное решение  линейного неоднородного уравнения (3.1), то для получения его общего решения необходимо найти общее решение соответствующего однородного уравнения . Тогда общее решение неоднородного уравнения записывается , т.е. общее решение получается при помощи одной квадратуры. В самом деле, подставляя  в уравнение (3.1), получаем:

,

 т. к. .

Значит,  и .

В ы в о д. Общее решение линейного неоднородного уравнения есть сумма его частного решения и общего решения соответствующего однородного уравнения.

3. Если известны любые два частных решения  и  линейного неоднородного уравнения (3.1), то его общее решение находится без квадратур и запишется .

Д о к а з а т е л ь с т в о. Так как  и  частные решения уравнения (3.1), то:

 и .

Поэтому, вычитая из первого равенства второе, находим:

 или .

Из последнего тождества следует, что  есть частным решением соответствующего однородного уравнения, а его общим решением будет функция . Тогда по второму свойству функция  будет общим решением уравнения (3.1).

К линейным уравнениям приводятся многие задачи современной техники.

П р и м е р 1. Конденсатор, емкость которого  включается в цепь с напряжением  и сопротивлением . Определить заряд  конденсатора в момент  после включения.

Р е ш е н и е. В момент  заряд конденсатора равен , и сила тока 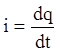. К этому моменту времени в цепи действует электродвижущая сила , равная разности между напряжением цепи  и напряжением конденсатора :

.

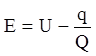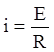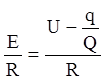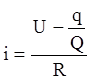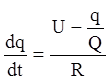По закону Ома сила тока  или  или  или  или .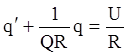

Интегрируя полученное линейное уравнение находим общее решение 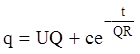. Согласно начальным условиям при , . Отсюда 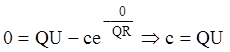. Итак, рассматриваемый процесс описывается уравнением:

.

3.3 Уравнения, сводящиеся к линейным

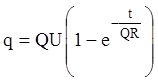Рассмотрим виды уравнений, которые при помощи некоторых преобразований можно свести к линейным.

1. Уравнения вида

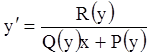,                             (3.15)

где , ,  - заданные функции,  можно свести к линейным уравнениям переходом от функции  к обратной к ней функции , .

Относительно этой функции из (3.15) и равенства , получаем линейное уравнение

.

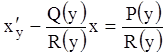П р и м е р 1. Решить уравнение:

.

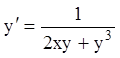Р е ш е н и е. Относительно функции  получим уравнение . Проинтегрировав, получим:

.

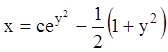2. Уравнения вида:

                    (3.16)

сводятся к линейным относительно функции  заменой

,                                      (3.17)

так как после замены получаем уравнение:

.

Решив последнее уравнение по формуле (3.14), получаем:

,

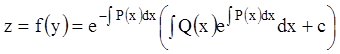т. е. получаем общий интеграл:

.                   (3.18)

П р и м е р  2. Проинтегрировать уравнение Бернулли:

, ,                     (3.19)

Очевидно, при  и  уравнение (3.19) линейное. Полагая что , делим уравнение на . Получаем:

.

Так как , то, положив , получим линейное уравнение:

,

которое решаем по формуле (3.14):

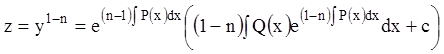.        (3.20)

Кроме того, уравнение Бернулли при  имеет решение . Это решение является особым при  и частным при .

З а м е ч а н и е. Уравнение (3.19) называют уравнением Якова Бернулли, так как он предложил его к решению в 1695 г. Лейбниц в 1696 г. указал на способ сведения его к линейному. Иоган Бернулли, младший брат Я. Бернулли, в 1697 г. нашел подстановку 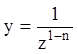, которая приводит уравнение (3.19) к линейному, и дал метод непосредственного интегрирования этого уравнения заменой , как и линейное уравнение.