Дифференциальные уравнения и математическое моделирование. Основные понятия дифференциальных уравнений. Метод Изоклин, страница 30

С геометрической точки зрения задача Коши для дифференциального уравнения второго порядка

             (7.6)

может быть истолкована как задача нахождения такой интегральной кривой, которая проходила бы через заданную точку  и имела бы в этой точке заданный угловой коэффициент касательной  .

С механической точки зрения нахождение решения задачи Коши для уравнения (7.4) с начальными условиями  может формулироваться так: найти такое движение, в котором движущаяся точка занимала бы в заданный (начальный) момент времени  заданное (начальное) положение и имела бы заданную (начальную) скорость .

Теорема существования и единственности решения задачи Коши определяет условия, при которых решение дифференциального уравнения n-го порядка существует и является единственным при заданных начальных условиях. Сформулируем эту теорему без доказательства.

Т е о р е м а   К о ш и – П и к а р а. Пусть дано дифференциальное уравнение (7.2) и начальные условия (7.5). Если функция

1)  непрерывная функция всех своих аргументов в области D, а следовательно ограничена ;

2)  удовлетворяет условию Липшица по аргументам ;

тогда уравнение (7.2) имеет единственное решение , удовлетворяющее заданным начальным условиям (7.5).

Условия теоремы Коши-Пикара выполняются, в частности, если функция f непрерывна на D и имеет в окрестности точки  ограниченные частные производные по .

Обратим внимание на то, что единственность решения задачи Коши для уравнения n-го порядка (7.2) не означает, что через данную точку  проходит только одна интегральная кривая, как это было для уравнения . Например, единственность решения задачи Коши (7.6) для уравнения второго порядка понимают в том смысле, что через точку  проходит единственная интегральная кривая уравнения, касательная к которой в точке  имеет угловой коэффициент , хотя через эту же точку  проходит еще бесчисленное множество интегральных кривых, но уже с другими наклонами касательных в этой точке.

П р и м е р 1. Материальная точка массы  падает по вертикальной прямой под действием силы тяжести, причем в некоторый начальный момент времени  известны ее положение  и скорость . Найти закон движения.

Р е ш е н и е. В качестве прямой падения выберем ось OY, начало координат поместим у поверхности Земли и ось OY направим вверх. Учитывая механический смысл второй производной, мы приходим к дифференциальному уравнению второго порядка  , где q – ускорение силы тяжести. Задача сводится к нахождению такого решения , которое удовлетворяет начальным условиям. Интегрируя уравнение, получаем:

.

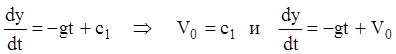Интегрируя еще раз, получаем 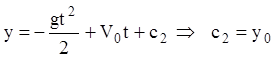  . Искомый закон движения имеет вид:  .

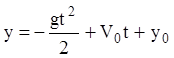Уточним некоторые понятия, определенные нами в начале курса. Пусть область D – область, в каждой точке которой задача Коши для уравнения (7.2) имеет единственное решение. Функция:

,                                              (7.7)

где  - произвольные постоянные, называется общим решением уравнения (7.2) в области D, если:

1)  функция  имеет непрерывные частные производные по x до n-го порядка включительно;

2)  для любой точки система:

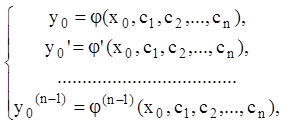                                           (7.8)

имеет единственное решение относительно :

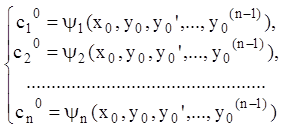                                           (7.9)

3)  функция   является решением уравнения (7.2) при любых значениях произвольных постоянных  в равенствах (7.9), когда точка  принадлежит области D.

Если общее решение (7.7) в области D задано неявно соотношением

,                                            (7.10)

то (7.10) называется общим интегралом уравнения (7.2) в области D.

Любое решение, получаемое из (7.7) при конкретных числовых значениях , называется частным решением уравнения (7.2).

В некоторых случаях нахождение общего решения уравнения (7.2) в явной или неявной форме представляет большие затруднения. В таких случаях, интегрируя уравнение (7.2), решение ищут в параметрическом виде:

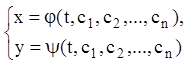,                                            (7.11)

где - произвольные постоянные. Такое решение уравнения (7.2) называют общим решением в параметрической форме.