Рассмотрим сначала однородное уравнение (3.2). Это уравнение с разделяющимися переменными, поэтому:
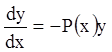 ;
; 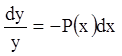 .
.
Проинтегрировав, получим ![]() ,
, ![]() или
или
![]() , (3.3)
, (3.3)
где ![]() -
произвольная постоянная. Из уравнения (3.2) следует, что
-
произвольная постоянная. Из уравнения (3.2) следует, что ![]() тоже является решением уравнения. Поэтому
решение (3.3) определяет общее решение уравнения (3.2) для
тоже является решением уравнения. Поэтому
решение (3.3) определяет общее решение уравнения (3.2) для ![]() .
.
Для решения линейного неоднородного уравнения (3.1) можно указать три способа.
![]() ,
(3.4)
,
(3.4)
где ![]() и
и ![]() - некоторые дифференцируемые функции от
- некоторые дифференцируемые функции от ![]() . Тогда
. Тогда ![]() .
Подставляя в уравнение (3.1), получаем
.
Подставляя в уравнение (3.1), получаем ![]() , или
, или
![]() . (3.5)
. (3.5)
Вполне понятно, что одну из функций ![]() или
или ![]() можно
выбрать произвольно. Значит, подберём
можно
выбрать произвольно. Значит, подберём ![]() так,
чтобы содержимое скобки уравнения (3.5) она обращала в ноль, т. е. была
решением уравнения:
так,
чтобы содержимое скобки уравнения (3.5) она обращала в ноль, т. е. была
решением уравнения:
![]() ,
(3.6)
,
(3.6)
откуда по формуле (3.3) имеем
![]() .
.
Для нашей цели достаточно иметь любое частное решение
уравнения (3.6), поэтому положим ![]() , и
, и
![]() .
(3.7)
.
(3.7)
Подставив найденное значение ![]() (3.7)
в уравнение (3.5) получим уравнение с разделяющимися переменными для нахождения
(3.7)
в уравнение (3.5) получим уравнение с разделяющимися переменными для нахождения
![]() :
:
![]() ,
, 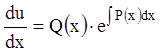
![]() . (3.8)
. (3.8)
Поэтому в силу (3.4), (3.7), (3.8) общее решение уравнения (3.1) будет:
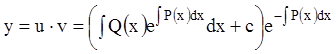 . (3.9)
. (3.9)
Этот способ применил Иоган Бернулли в 1697 г. Лейбниц
же умел решать линейное уравнение подстановкой ![]() немного
раньше Бернулли (1693 г.).
немного
раньше Бернулли (1693 г.).
П р и м е р 1. Решить задачу Коши:
![]() ,
, ![]() .
.
Р е ш е н и е. Это линейное уравнение, так как его
можно представить в виде 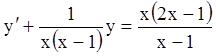 . Поэтому замена
. Поэтому замена ![]() ,
, ![]()
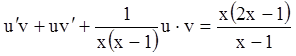 ;
;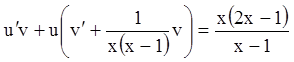 ;
;
![]() :
: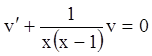 ;
;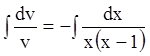 ;
;![]() ;
;
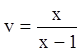 .
.
![]() :
: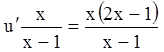 ;
;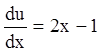 ;
;![]() ;
;
![]() ;
; ![]() .
.
Следовательно, общее решение 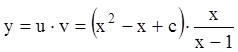 ,
или
,
или 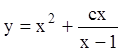 - общее решение. Используя начальное
условие, для нахождения
- общее решение. Используя начальное
условие, для нахождения ![]() получаем:
получаем: 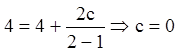 . Решением задачи Коши будет
. Решением задачи Коши будет ![]() .
.
О т в е т: ![]() .
.
Суть этого метода такая: общее решение уравнения (3.1)
будем искать в виде (3.3), рассматривая ![]() как
функцию от
как
функцию от ![]() , т. е.
, т. е. ![]() и
и
![]() . (3.10)
. (3.10)
Подставим (3.10) в (3.1), предварительно вычислив
![]() ;
;
![]() .
.
Поэтому
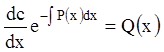 ;
; ![]() ;
;
![]() . (3.11)
. (3.11)
Подставив (3.11) в (3.10), получаем общее решение
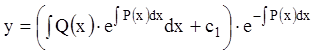 .
(3.12)
.
(3.12)
П р и м е р 1. Решить уравнение
![]() .
.
Р е ш е н и е. 1) Решаем соответствующее однородное
уравнение ![]() ;
;  ;
; 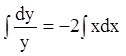 ;
; ![]() или
или ![]() .
.
2) Общее решение неоднородного уравнения ищем в виде ![]() , где
, где ![]() -
неизвестная функция.
-
неизвестная функция. ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() . Тогда общее решение
. Тогда общее решение ![]() - общее решение.
- общее решение.
З а м е ч а н и е 1. Метод вариации произвольной постоянной разработан также И. Бернулли и опубликован в 1697 г., однако этот метод связывается не с его именем, а с именем Лагранжа. Это можно объяснить тем, что именно Лагранж в 1774-1775 г.г. разработал метод вариации произвольных постоянных для линейного уравнения n-го порядка.
З а м е ч а н и е 2. Линейное уравнение ![]() может иметь особые решения вида
может иметь особые решения вида ![]() , где
, где ![]() -
корень уравнения
-
корень уравнения ![]() .
.
Общее решение неоднородного линейного дифференциального уравнения (3.1) находим, умножая это уравнение на интегрирующий множитель
![]() .
(3.13)
.
(3.13)
В результате получаем
![]() .
.
Так как левая часть этого уравнения представляет собой
производную выражения ![]() , то
, то 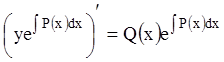 , или
, или 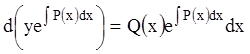 . Интегрируя последнее равенство, получаем:
. Интегрируя последнее равенство, получаем:
![]() ,
,
откуда искомое общее решение:
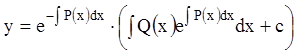 .
(3.14)
.
(3.14)
Общее решение (3.14) полностью совпадает с общими решениями (3.9) и (3.12), полученными другими методами.
П р и м е р 1. Решить уравнение
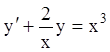 .
.
Р е ш е н и е. В данном случае  ,
,
![]() , поэтому
, поэтому 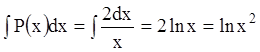 .
Следовательно, интегрирующий множитель
.
Следовательно, интегрирующий множитель ![]() .
Умножая данное уравнение на
.
Умножая данное уравнение на ![]() , получаем:
, получаем:
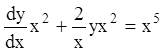 ;
; ![]() .
.
Поскольку в левой части равенства образовался
дифференциал от произведения ![]() , то
, то ![]() , интегрируя, получаем
, интегрируя, получаем ![]() ;
; 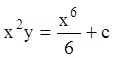 ;
;  - общее решение.
- общее решение.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.