![]() -
-
- поток вектора ![]() через всякую замкнутую
поверхность, не охватывающую заряд
через всякую замкнутую
поверхность, не охватывающую заряд ![]() , равен нулю:
, равен нулю:
![]()
Полученные результаты справедливы для любой систему
электрических зарядов. Действительно, пусть поле образовано системой зарядов ![]() . Согласно принципу суперпозиции,
напряженность результирующего поля
. Согласно принципу суперпозиции,
напряженность результирующего поля ![]() Поток
результирующего вектора
Поток
результирующего вектора ![]() равен
равен
![]() ,
,
где ![]() , и
, и
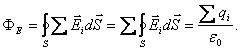
Эта формула выражает собой теорему Гаусса:
В произвольном электростатическом поле в вакууме
поток вектора напряженности ![]() через
произвольную замкнутую поверхность равен алгебраической сумме зарядов,
расположенных внутри этой поверхности, деленной на электрическую постоянную
через
произвольную замкнутую поверхность равен алгебраической сумме зарядов,
расположенных внутри этой поверхности, деленной на электрическую постоянную ![]() .
.
Если сумма ![]() , то
, то ![]() - линии напряженности выходят
из поверхности, если
- линии напряженности выходят
из поверхности, если ![]() ,
, ![]() -
линии напряженности входят в поверхность. Из теоремы Гаусса следует:
-
линии напряженности входят в поверхность. Из теоремы Гаусса следует:
1. Линии напряженности могут начинаться только в местах положительных зарядов, а заканчиваться только в местах отрицательных зарядов.
2. Если мы возьмем замкнутую поверхность, охватывающую заряды, алгебраическая сумма которых равна нулю, то полный поток вектора напряженности через поверхность равен нулю. Это означает, что число линий, выходящих из объема, ограниченного данной поверхностью, равно числу линий, входящих в объем.
3. Если замкнутая поверхность проведена в поле так, что внутри нее нет зарядов, то линии напряженности будут ее пронизывать, не начинаясь, и не кончаясь внутри нее. Следовательно, число входящих линий равно числу выходящих линий, и полный поток напряженности через поверхность также равен нулю.
Рассмотрим
теперь дифференциальную форму теоремы Гаусса. Пусть в некоторой точке ![]() с координатами
с координатами ![]() напряженность поля (рис.1.1.9)
равна
напряженность поля (рис.1.1.9)
равна ![]() . Построим около точки
. Построим около точки ![]() прямоугольный бесконечно
малый параллелепипед объемом
прямоугольный бесконечно
малый параллелепипед объемом ![]() . Объемная плотность заряда в нем равна
. Объемная плотность заряда в нем равна ![]() и зависит от координат выбранной
точки поля:
и зависит от координат выбранной
точки поля: ![]() .
.
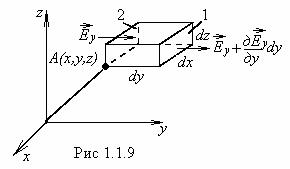 Поток вектора
Поток вектора ![]() через правую
грань (1)
через правую
грань (1)
равен:
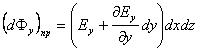 ,
,
а через левую (2):
![]() ,
,
Поэтому поток вдоль оси ![]() равен
равен
![]()
Таким же образом для верхней и нижней грани получим:
![]() ,
,
для задней и передней:
![]() .
.
По теореме Гаусса
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.