Анализ динамических систем методом математического моделирования: Методические указания по выполнению лабораторной работы

Министерство образования и науки Российской Федерации

Федеральное агентство по образованию

Саратовский государственный технический университет

Балаковский институт техники, технологии и управления

Анализ динамических систем  

методом математического моделирования

Методические указания

по выполнению лабораторной работы

для студентов специальности 120100

всех форм обучения

Одобрено

                          редакционно-издательским советом

                     Балаковского института  техники

              технологии и управления

Балаково  2008

Введение

При  исследовании динамических систем они описываются дифференциальными уравнениями. Для решения даже относительно простых дифференциальных уравнений требуется большое количество вычислений. Поэтому практическое исследование динамических систем невозможно без использования вычислительной техники. В данной работе на примере дифференциального уравнения второго порядка рассматриваются решения дифференциальных уравнений методом математического моделирования в системе Simulink MatLab.

1.  Построение математической модели динамической системы

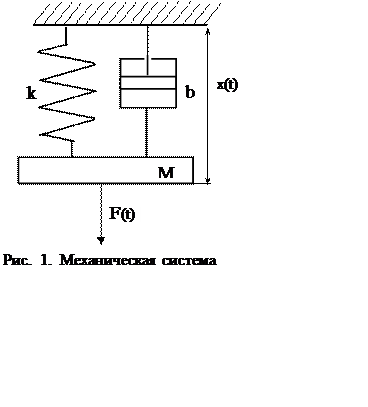
На механическую систему, содержащую пружину жесткостью k, демпфер с коэффициентом вязкости b, тело массой M (рис. 1) действует сила F(t). Необходимо построить математическую модель, описывающую движение системы во времени. 

Входной переменной является сила, действующая на систему .

За выходную переменную примем положение подвижной массы М относительно базовой поверхности  x(t).  Структурная схема системы приведена на рис.2.

Составим уравнение движения на основе второго закона Ньютона, согласно которому момент инерции системы равен сумме сил, действующих на систему.

Момент инерции системы равен    .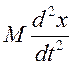

Сила упругости пружины на  основании закона Гука пропорциональна деформации пружины    .

Сила сопротивления движению поршня демпфера на основании закона Ньютона для идеальной жидкости пропорциональна скорости движения поршня демпфера        .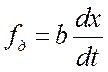

Тогда уравнение равновесия Ньютона

                                    .

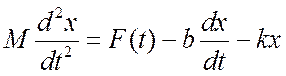Приведем уравнение к стандартному виду, когда все выходные координаты находятся в левой части, входные – в правой части, а коэффициент при выходной переменной равен единице

                                  .

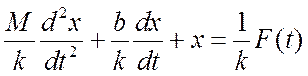Мы получили дифференциальное уравнение второго порядка.

2.  Решение дифференциального уравнения методом математического моделирования в системе Simulink

Разрешим дифференциальное уравнение относительно старшей производной                   .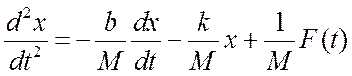

Считая, что вторая производная выходной переменной  известна, проинтегрируем ее два раза и получим     .

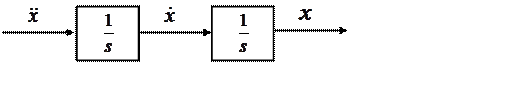Рассчитаем вторую производную выходной переменной путем суммирования элементов правой части уравнения.  Подав выход сумматора на вход первого интегратора, получим структурную схему системы, решающую данное дифференциальное уравнения (рис. 3).

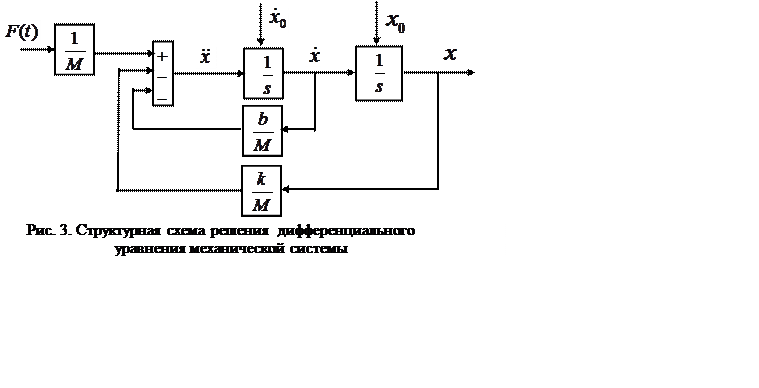
Особенностью данной схемы является необходимость для нахождения второй производной выходной переменной знания этой второй производной. Это условие компенсируется заданием начальных значений первой производной и самой выходной переменной, которые называются начальными условиями .

В общем случае решение дифференциального уравнения является суммой двух составляющих  . В зависимости от начального состояния системы и наличия входного воздействия могут быть различные случаи движения системы.

1. Свободное движение системы определяет движение системы из заданного начального состояния () в установившееся состояние при отсутствии входного воздействия и описывается свободной составляющей   .

Пример 1.  Массу М сместили  на  какое-то расстояние   и отпустили.  Под действием пружины система придет в движение. Движение системы в данном случае описывается свободной составляющей при ненулевом начальном отклонении   и нулевой начальной скорости .

Пример 2. Массу сместили на какое-то начальное отклонение и толкнули с постоянной скоростью. Движение системы в данном случае описывается свободной составляющей при заданном начальном отклонении   и заданной начальной скорости .

2. Вынужденное движение системы из начального состояния (с нулевыми начальными условиями). При воздействии на систему, находящуюся в начальном состоянии внешней силы F(t)   движение системы  описывается вынужденной  составляющей . При этом закон движения системы зависит от зависимости изменения внешней силы во времени.

Пример 1. На систему вниз стала действовать постоянная сила . Движение массы М вниз до уравновешивания действующей силы   силой упругости пружины  описывается вынужденной составляющей.

Пример 2. На систему действует синусоидальное входное воздействие  . Система из состояния покоя перейдет в новое установившееся состояние, которым будет синусоидальное движение системы с круговой частотой   и амплитудой, зависимой от амплитуды входного воздействия и параметров системы .

3. Вынужденное движение системы с ненулевыми начальными условиями.  Данное движение описывается суммой свободного и вынужденного движений  и зависит от начальных условий и закона изменения во времени входного воздействия.

3.  Операторный метод решение дифференциального уравнения

                                  на основе передаточной функции

Для решения дифференциальных уравнений широко применяется  операторный метод. Запишем  полученной дифференциальное уравнение механической системы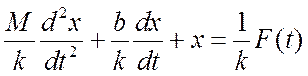              

Данное уравнение содержит три величины:

1  Функцию изменения во времени входного сигнала .

2  Функцию изменения во времени выходного сигнала .

3  Само дифференциальное уравнение, являющееся оператором преобразования входной функции времени  в выходную функцию времени .

          В основе операторного метода решения дифференциальных уравнений лежит преобразование Лапласа. При этом производится  преобразование временных функции   и дифференциального уравнения в функции  и оператор комплексной переменной      ().

Прямое преобразование Лапласа   .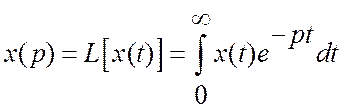

 называется изображением по Лапласу временной функции

Обратное преобразование Лапласа имеет вид  .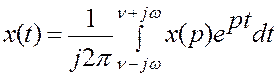

Алгоритм  решения задачи символическим методом заключается в следующем (рис. 4):

1. Записывается  дифференциальное уравнение, описывающее закономерности рабаты динамического звена

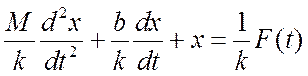
2. Делается преобразование дифференциального уравнения по Лапласу в оператор комплексной переменной

          1) вместо записываются функции комплексной переменной  

                ,

          2) В дифференциальном уравнении производные  первого, второго и т.д. порядков заменяются на  оператор 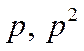 и т.д., а именно,   

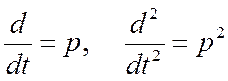           и т.д.,   

например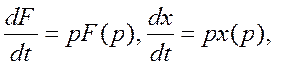        

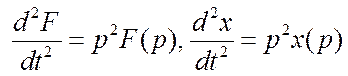
          В данном случае преобразованное по Лапласу уравнение имеет вид

                           .

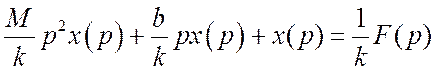          Оно является алгебраическим. Умножение в комплексной плоскости на оператор означает, что во временной плоскости производится дифференцирование. Деление в комплексной плоскости на оператор означает обратное действие - интегрирование.

3. Находится преобразование Лапласа  от закона изменения входной переменной                .

          Для этого существуют таблицы преобразования Лапласа в справочниках, а также команды символьных преобразований в математических процессорах компьютеров.