4. Полученное алгебраическое
уравнения решается относительно выходной переменной ![]()
5. Находится обратное
преобразование Лапласа от ![]()
![]() ,
,
которое является искомым решением ![]() и описывает изменение во времени
выходной переменной.
и описывает изменение во времени
выходной переменной.
Преобразование Лапласа дифференциального уравнения приводит к удобному и широко применяемому выражению связи между изображениями входной и выходной величин через передаточную функцию.
Рассмотрим выражение, полученное после применения преобразования Лапласа к дифференциальному уравнению,
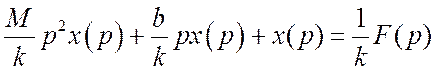
В левой части ![]() является множителем и его можно
вынести за скобки
является множителем и его можно
вынести за скобки
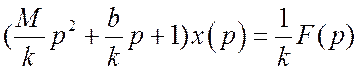
Найдем отношение 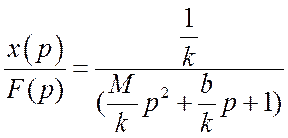
Отношение
изображения выходной величины системы к изображению входной величины называется
передаточной функцией и обычно обозначается ![]() .
В данном случае передаточная функция равна
.
В данном случае передаточная функция равна
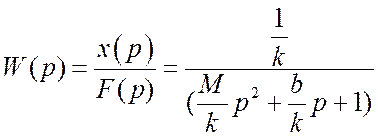
При известной
передаточной функции изображение выходной пере менной находится как
произведение передаточной функции на изображение входной переменной ![]() .
.
что существенно упрощает анализ элементов и систем управления.
В системе MatLab при использовании передаточной функции входная
переменна ![]() и выходная переменна
и выходная переменна ![]() автоматически преобразуются по
Лапласу без участия исследователя. Схема моделирования рассмотренной системы на
основе передаточной функции имеет вид, представленный на рис. 5. Следует
отметить условность схемы, т.к. передаточная функция относится к
преобразованиям Лапласа входной и выходной величин
автоматически преобразуются по
Лапласу без участия исследователя. Схема моделирования рассмотренной системы на
основе передаточной функции имеет вид, представленный на рис. 5. Следует
отметить условность схемы, т.к. передаточная функция относится к
преобразованиям Лапласа входной и выходной величин ![]() .
Кроме того, следует отметить, что передаточная функция описывает зависимость
выходной переменной от входной только при нулевых начальных условиях.
.
Кроме того, следует отметить, что передаточная функция описывает зависимость
выходной переменной от входной только при нулевых начальных условиях.
4 Порядок выполнения лабораторной работы
4.1
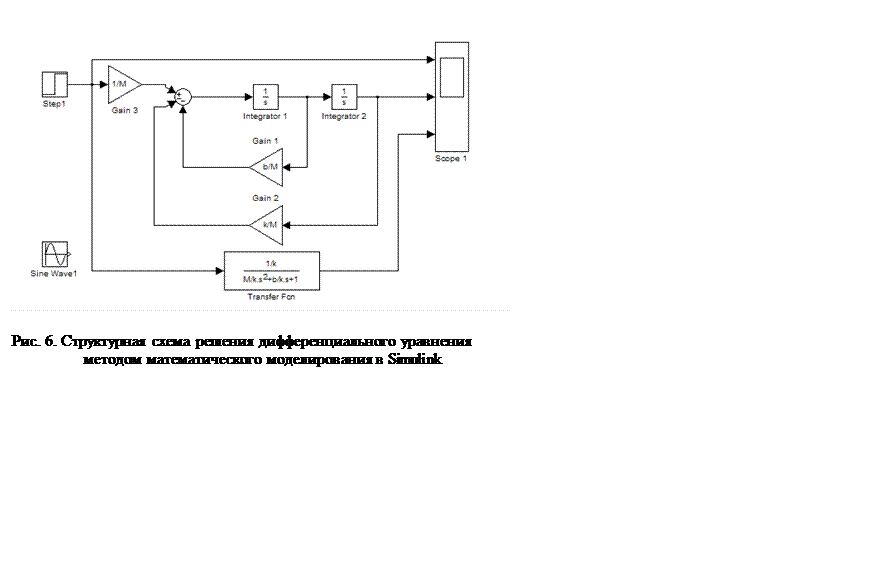
В Simulink MatLab вводится модель,
приведенная на рис. 6. Модель включает схему моделирования построенного
дифференциального уравнения механической системы и передаточную функцию по
каналу входное усилие ![]() на перемещение массы груза
на перемещение массы груза
![]() .
.
4.2
Из таблицы вариантов заданий выбираются значений параметров механической
системы ![]() .
.
4.3
В системе MatLab вводятся
значения параметров ![]() . Для рассматриваемого
примера
. Для рассматриваемого
примера ![]() .
.
4.4
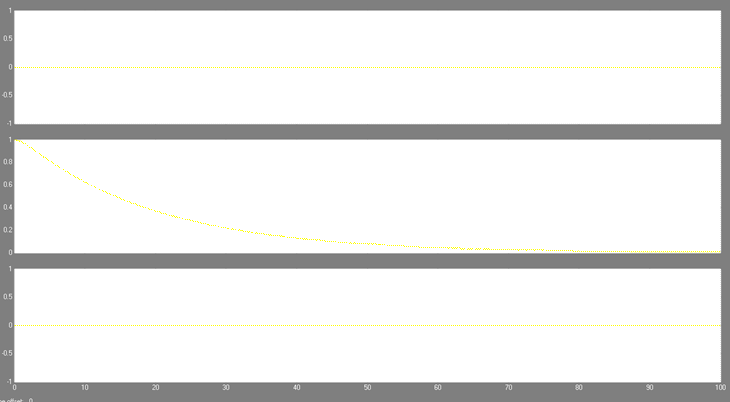
Анализ свободного движения системы при единичном начальном условии по положению
(на втором интеграторе вводится начальное значение Initial Cjndition, равное 1). Для значений с
различными коэффициентами демпфирования (для рассматриваемого примера ![]() ) производится моделирование системы
и сравнивается вид кривых переходных процессов из заданного начального
положения в нулевое положение. Графики переходных процессов переносятся в отчет
(Рис. 7). Обратить внимание, что выходной сигнал передаточной функции не реагирует
на начальные условия.
) производится моделирование системы
и сравнивается вид кривых переходных процессов из заданного начального
положения в нулевое положение. Графики переходных процессов переносятся в отчет
(Рис. 7). Обратить внимание, что выходной сигнал передаточной функции не реагирует
на начальные условия.
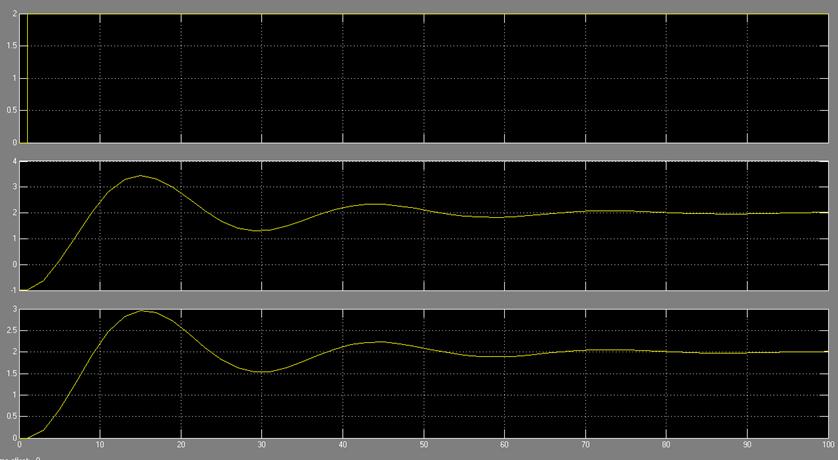
4.5
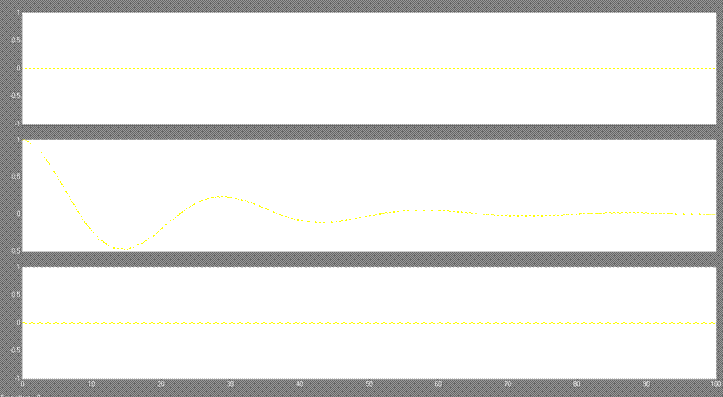
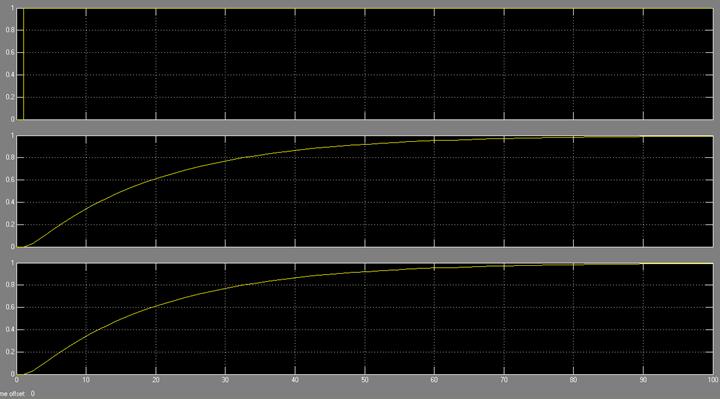
Анализ переходного процесса системы при различных значениях коэффициента
демпфирования. На вход системы подается единичный ступенчатый сигнал при
нулевых начальных условиях и снимается переходной процесс при трех увеличивающихся
в 10 раз значениях параметра демпфирования. Для приведенных данных ![]() . Для каждого значения
. Для каждого значения ![]() фиксируется переходной процесс и
анализируется его влияние на вид кривой переходного процесса (рис. 8). Обратить
внимание на совпадение решений дифференциального уравнения и выходного сигнала
передаточной функции.
фиксируется переходной процесс и
анализируется его влияние на вид кривой переходного процесса (рис. 8). Обратить
внимание на совпадение решений дифференциального уравнения и выходного сигнала
передаточной функции.
4.6
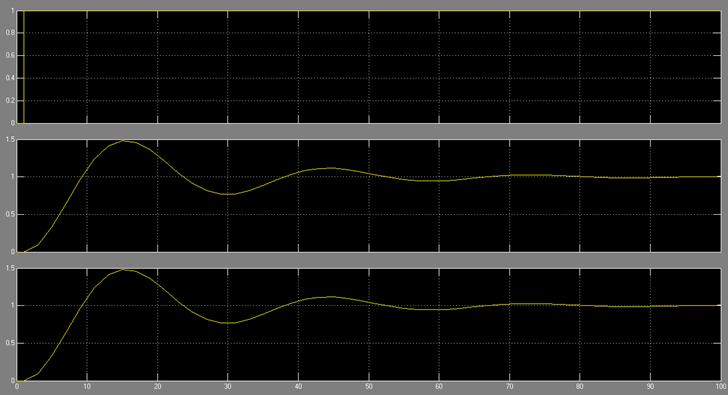
Анализ переходного процесса системы при различных значениях коэффициента
демпфирования. На вход системы подается единичный ступенчатый сигнал при
нулевых начальных условиях и снимается переходной процесс при трех
увеличивающихся в 10 раз значениях параметра демпфирования. Для приведенных
данных ![]() . Для каждого значения
. Для каждого значения ![]() фиксируется переходной процесс и
анализируется его влияние на вид кривой переходного процесса (рис. 9).
Обратить внимание на совпадение решений дифференциального уравнения и выходного
сигнала передаточной функции.
фиксируется переходной процесс и
анализируется его влияние на вид кривой переходного процесса (рис. 9).
Обратить внимание на совпадение решений дифференциального уравнения и выходного
сигнала передаточной функции.
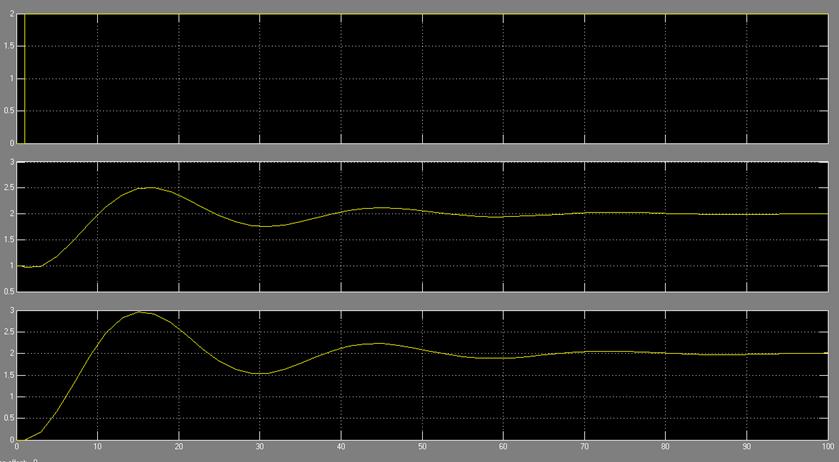
4.7 Провести моделирование системы при ступенчатом входном сигнале и ненулевых начальных условиях. Зафиксировать переходные процессы, сравнить решение дифференциального уравнения и выход передаточной функции (рис. 8).
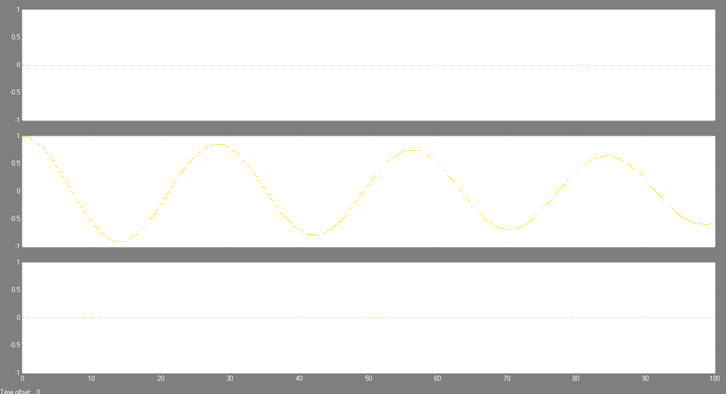
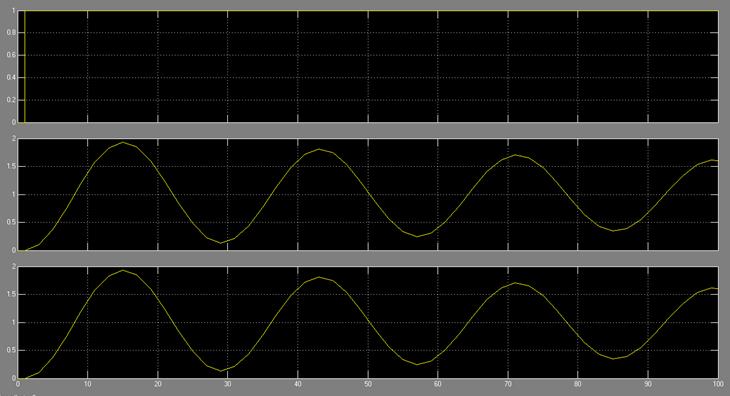
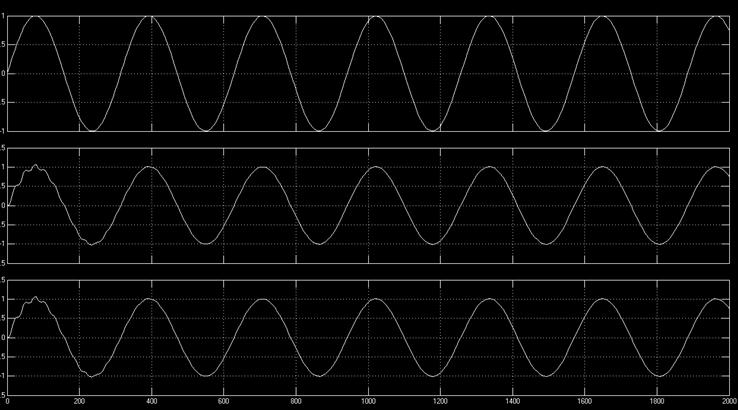
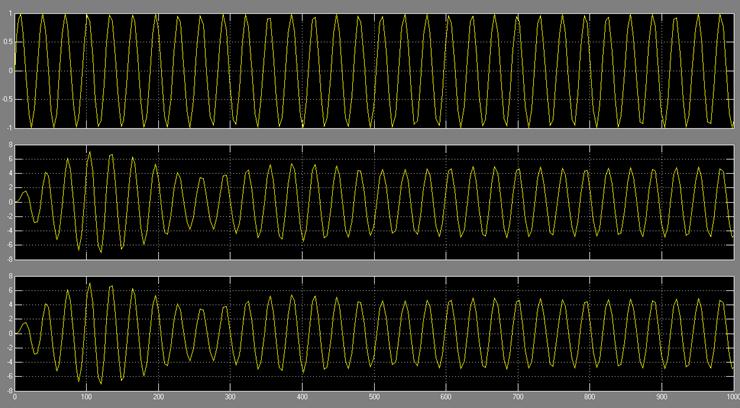
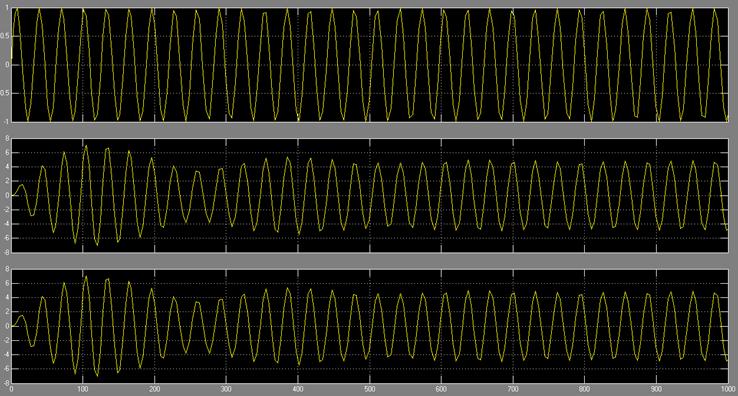
4.8 Анализ коэффициента передачи системы от частоты входного сигнала. На вход системы подключается источник синусоидального сигнала. Производится моделирование и записывается выходной сигнал системы при изменении частоты входного сигнала, которая принимается равной
![]() .
.
Для каждой частоты фиксируется график выходной переменной и рассчитывается отношение амплитуды выходного сигнала к амплитуде входного сигнала (рис. 10). Изменение коэффициента передачи при изменении частоты входного сигнала называется амплитудной частотной характеристикой системы. Обратить внимание на совпадение решения дифференциального уравнения и выходного сигнала передаточной функции.
4.9 Оформить отчет. Отчет должен содержать титульный лист, постановку задачи работы, построение математической модели механической системы, исходные данные, полученные графики, обсуждение, выводы по результатам работы.
Список использованной литературы.
1. Черных И.В. SIMULINK. Среда создания инженерных приложений.–М.: Диалог МИФИ, 2004.- 496с.
2. Дэбни Дж. Харман Т. SIMULINK 4. Секреты мастерства. –М.: Бином, 2003.- 403с.
3. Дьяконов В.П. Simulink 4. Специальный справочник.- СПб.: Питер, 528с.
 |
|
|
|
|
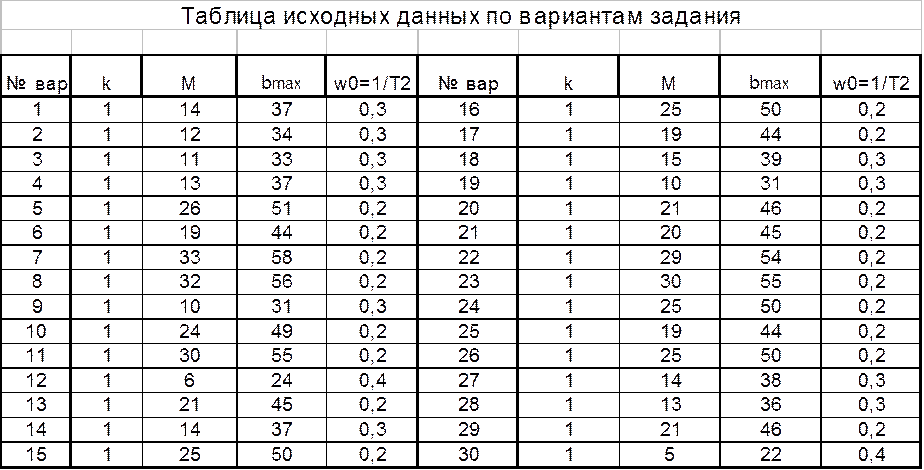
Анализ динамических систем
методом математического моделирования
Методические указания
по выполнению лабораторной работы
для студентов специальности ТАМ
Составил:
Бирюков Владимир Петрович
Рецензент О.В. ВИШТАК
Корректор А.М. Рогачева
Редактор Л.В. Максимова
Подписано в печать Формат 60х84 1/16
Бум. тип. Усл. печ. л. Уч.-изд.л
Тираж 150 экз. Заказ Бесплатно
Саратовский государственный технический университет
410054, г. Саратов, ул. Политехническая, 77

Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.