Для получения коэффициентов деления, дополняющих ряд положительных целых чисел до полного, используются ЛС, позволяющие увеличить период исходной импульсной последовательности в (2b+ 1) раз (рис. 6.68). Эта схема состоит из логической схемы делителя на 2b (основной триггер Тг0) и дополнительного триггера (ТгД), включенного в так называемую цепь логической ОС (ЛОС). Рассмотрим работу схемы, положив для определенности и простоты b= 1.
На рис. 6.69 показаны временные диаграммы работы схемы, причем точкам а, б и в на рис. 6.68 соответствуют графики а, б и в. Будем считать, что в момент включения на выходе Q Тг0 (точка б) сигнал отсутствует, а на выходе Q триггера Тг0 (точка б) сигнал имеется. Тогда при поступлении на вход (точка а) импульса на выходе триггера Тг0 (точка б) появится сигнал, который удержится до начала следующего импульса исходной последовательности, так как при отсутствии сигала на входе С триггер сохраняет свое состояние. В течение этого времени сигнал сохранится и на выходе Q триггера ТгД вначале как результат режима установки нуля, а затем - режима запуска.
При появлении второго импульса исходной последовательности в обоих триггерах устанавливается режим счета, и на их выходах сигнал исчезает. Третий импульс исходной последовательности не вызовет появления сигнала на выходе Тг0 поскольку триггер находится в режиме установки нуля. Этот же режим устанавливается и в триггере ТгД и поэгому на его инверсном выходе появляется сигнал. Четвертый импульс устанавливает в Тго режим счета, вследствие чего на его выходе появляется сигнал, и т. д. В результате на выходах триггеров возникают последовательности импульсов с периодами 3То, любая из которых пригодна для реализации ДЧ с коэффициентом n=21 +1=3. В рассматриваемой схеме выходной является последовательность на выходе Тгд.
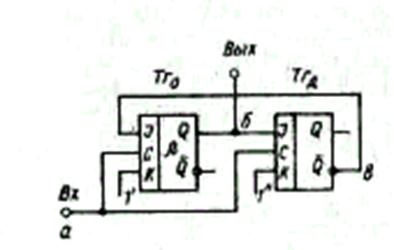
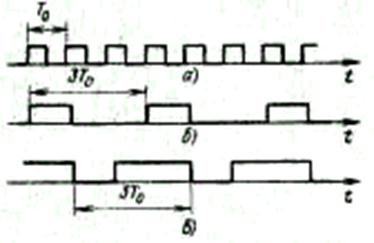
Рис. 6.68. Схема делителя
на (2b+1)
Рис. 6.69. Временные диаграммы работы делителя на (2b+ 1)
Если вместо одного триггера Тго использовать ЛС делителя на 2b, то период выходной последовательности будет больше периода входной в 2b+1 раз. Другими словами, схема будет представлять собой ЛС делителя частоты в п =2b+1раз.
На основе ЛС делителей на 2a и 2b+1 может быть получена обобщенная логическая схема ДЧ на любое целое число. Синтез этой схемы начинается приведением числа п к следующему виду:
![]() ,
,
где a- любое целое положительное число; Аi- нуль или единица. На основе этого разложения синтезируется ЛС по правилам, которые иллюстрируются рис. 6.70.
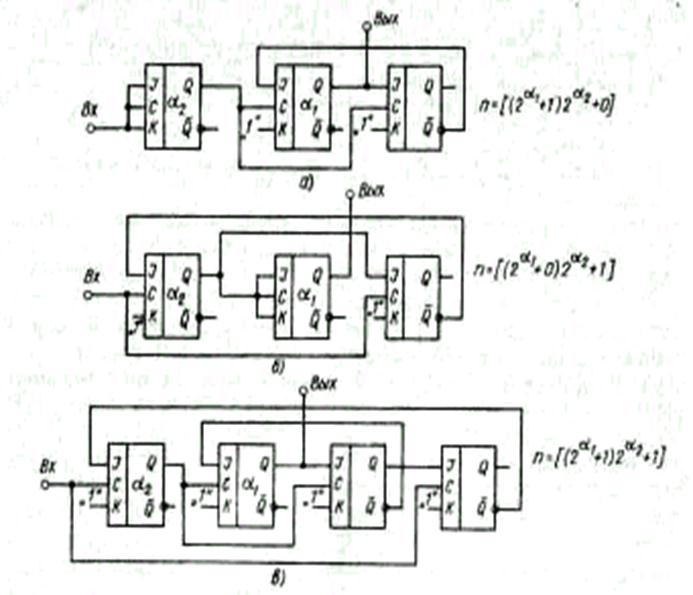
Рис.6.70. К синтезу обобщенной логической схемы делителя
частоты на любое целое число
Логическая схема ДЧ на дробно рациональное число q имеет структуру, показанную на рис. 6.71. В состав этой схемы входят логические схемы ДЧ на целые числа п (ЛС1) и т (ЛС2) схемы И и Не. Работает схема следующим образом. Исходная последовательность импульсов частотой fо подается на ДЧ с коэффициентами деления п и т. Последовательность импульсов с выхода делителя на n, частота следования которой равна fо/n поступает на схему И, на второй вход которой подается инвертированная последовательность с частотой следования fо/т. Инвертирование этой последовательности осуществляет схема Не. В результате работы схем логических И и Не происходит амплитудная манипуляция последовательности fо/п последовательностью fо/m.
Наибольшую амплитуду сформированной таким
способом выходной импульсной последовательности имеют составляющие спектра с
частотами ![]() . Очевидно, что выделение из
спектра составляющей с частотой fH=f0/n-f0/m соответствует результату деления исходной частоты f0 на коэффициент
q=mn/(m-n).
. Очевидно, что выделение из
спектра составляющей с частотой fH=f0/n-f0/m соответствует результату деления исходной частоты f0 на коэффициент
q=mn/(m-n).
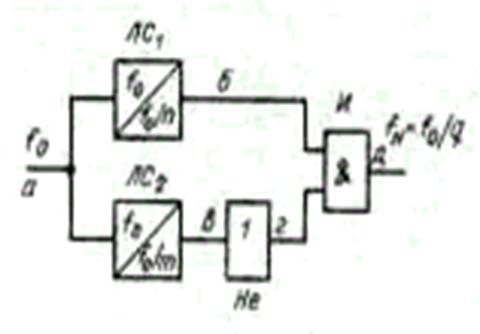
Рис. 6.71. Делитель на дробно рациональное число q
В качестве примера на рис. 6.72 приведены временные диаграммы делителя на q=10/3(n=2,m=5). Буквенные обозначения диаграмм совпадают с обозначениями точек в схеме на рис. 6.71, где наблюдаются соответствующие последовательности импульсов.
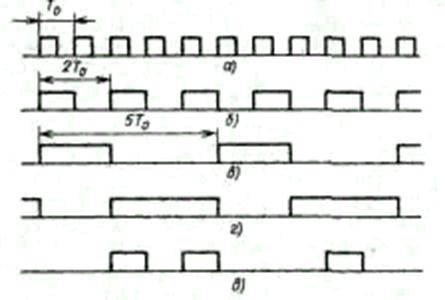
Рис. 6.72. Временные диаграммы делителя на q= 10/3
Анализ ЛС для делителей на дробно-рациональные числа посредством разложения их выходных импульсных последовательностей в ряд Фурье позволяет установить, что затухание полезного продукта относительно полной мощности выходной последовательности составляет около 4 дБ, а затухание ближайшего по частоте паразитного продукта, отстоящего на интервал fо/m не менее 9 дБ. При проектировании для этих делителей фильтров следует учитывать наличие в спектре выходной импульсной последовательности составляющей 2fо/m , амплитуда которой равна полезной составляющей.
В ГО многоканальных СП прошлых поколений широко использовались регенеративные ДЧ. Последние представляют собой замкнутые колебательные системы, при работе которых имели место не только балансы амплитуд и фаз, но и частоты (рис. 6.73).
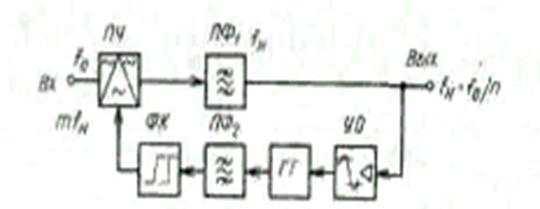
Рис.6.73. Регенеративный делитель частоты
В схеме на рис. 6.73 УО обеспечивает баланс
амплитуд, а фазовый корректор (ФК) - баланс фаз по петле ОС.
Гармонический генератор совместно с ПФ2 является умножителем частоты
fн на т. На входе системы установлен
преобразователь частоты (ПЧ), полезную составляющую на выходе которого с частотой
fH=f0/n выделяет ПФ1. В зависимости
от того, какой сигнал принят модулирующим (fо или
mf), а также в зависимости от режима работы ПЧ на
выходе ДЧ fH=f0/n будет определяться либо по
формуле ![]() либо
либо ![]() ,
где f0- частота исходного сигнала; т- номер
гармоники, выделяемой ПФ (коэффициент умножения частоты fн); r-номер используемой боковой полосы на выходе ПЧ.
,
где f0- частота исходного сигнала; т- номер
гармоники, выделяемой ПФ (коэффициент умножения частоты fн); r-номер используемой боковой полосы на выходе ПЧ.
Учитывая, что fH=f0/n из этих выражений находим, что коэффициент деления n=(m-1)/r или n=rm+1. Необходимо заметить, что при определении п отбрасывались решения, где fн отрицательна или больше исходной.
Из первой формулы для п следует, что коэффициент деления может быть дробно рациональным числом. В том случае, когда коэффициент деления должен быть целым числом, удобно использовать схему, для которой п определяется по второй формуле. Объясняется это тем, что иногда (когда п невелико) из схемы могут быть исключены ГГ и ПФ.
В настоящее время регенеративные ДЧ находят ограниченное применение, поскольку из-за того, что они содержат больше аналоговых устройств по сравнению с цифровыми, их надежность ниже, а стоимость выше.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.