На рис. 6.61, д изображена осциллограмма тока катушки индуктивности iL=i1-i2. Здесь же показаны значения токов i"+ и i"-, при которых наступает насыщение ферромагнитного сердечника, и значения i'+ и i'-, при которых сердечник выходит из состояния насыщения .
Следует заметить, что графики на рис. 6.60 и 6.61 не отражают того факта, что разряд конденсатора С происходит в реальных условиях не на активное сопротивление нагрузки Rн, а на комплексное Zн, поскольку нагрузкой обычно является несколько параллельно соединенных полосовых фильтров, настроенных на различные гармоники частоты f0.
Кроме того, в некоторых случаях приходится
учитывать конечные значения сопротивления источника сигнала R0 и индуктивности катушки в состоянии насыщения Lн.
Однако для ориентировочной оценки амплитуд отдельных гармоник достаточно
проанализировать еще более упрощенную форму выходного тока i2, представляющую собой последовательность с периодом Т0=1/2f0p биполярных экспоненциальных импульсов с нулевым
временем нарастания фронта и спадом, происходящим по закону ![]() , где
, где ![]() (рис.
6.62).
(рис.
6.62).
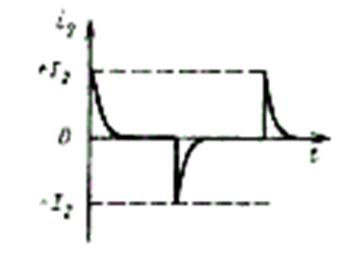
Рис. 6.62. Последовательность экспоненциальных импульсов
Разложение этой функции в ряд Фурье содержит только нечетные гармоники частоты f0. Относительная величина амплитуды (2к+ 1)-й гармоники
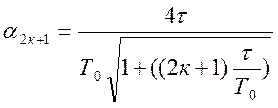
На рис. 6.63 приведены графики, показывающие зависимость амплитуды гармоники от ее номера и значения отношения t/Т0. Из рисунка видно, что уменьшение постоянной времени т приводит к выравниванию амплитуд гармоник за счет уменьшения амплитуд гармоник низких номеров. Этот случай имеет место при снижении т за счет уменьшения емкости С. Если же t снижать за счет уменьшения сопротивления нагрузки, то выравнивание амплитуд будет происходить за счет как увеличения амплитуд гармоник низких номеров, так и уменьшения амплитуд высших гармоник.
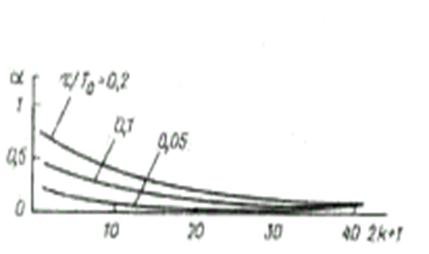
Рис. 6.63. Графики зависимости амплитуды гармоники
от ее номера и значения отношения t/Т0
Поскольку выходной сигнал ГГ содержит только нечетные гармоники частоты f0, то для получения четных гармоник приходится использовать схему удвоения, представляющую собой двухполупериодный диодный выпрямитель (рис. 6.64).
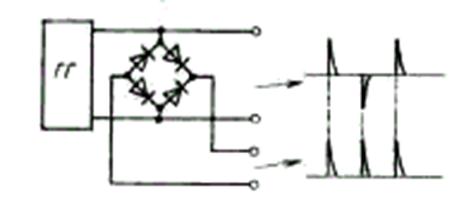
Рис.6.64. Схема двухполупериодного диодного выпрямителя
На выходе выпрямителя ток будет иметь форму униполярных импульсов с периодом вдвое меньшим периода основной частоты f0. Такие импульсы содержат как четные, так и нечетные гармоники частоты 2f0 или, что то же самое, только четные гармоники частоты f0. Получение четных и нечетных гармоник на различных выходах упрощает их разделение.
В заключение заметим, что схему, формирующую экспоненциальные импульсы по принципу заряд - разряд, можно реализовать, например, на транзисторном ключе. Однако рассмотренная схема на катушке индуктивности с ферромагнитным сердечником до настоящего времени оказывается непревзойденной по надежности работы в условиях относительно больших мощностей выходного сигнала и относительно высоких скоростей переключения схемы в разные состояния.
Делители частоты
В настоящее время все большее распространение в генераторном оборудовании многоканальных СП получают делители частоты (ДЧ) на логических элементах (цифровые ДЧ). Структурная схема цифрового ДЧ приведена на рис. 6.65. Она состоит из усилителя-ограничителя (УО), логической схемы (ЛС) и полосового фильтра (ПФ).
Усилитель-ограничитель формирует из входного синусоидального сигнала частотой Уц последовательность униполярных прямоугольных импульсов той же частоты и, следовательно, с периодом Т0=1/2f0p.
Логическая схема формирует на основе исходной последовательности новую периодическую последовательность импульсов, в спектре которой содержится составляющая необходимой частоты fH=f0/n достаточно высоким уровнем.
Полосовой фильтр выделяет полезную синусоидальную составляющую частоты fн.
Коэффициент деления п может быть как целым, так и дробно рациональным числом, что определяется структурой ЛС и полосой пропускания ПФ.
Логическая схема целочисленного делителя частоты (n-целое число) должна формировать последовательность прямоугольных импульсов с периодом Тн=nТ0, поскольку в спектре такого сигнала наибольшую величину имеет именно полезная составляющая, т. е. составляющая с частотой fн=1/2Тнp=f0/n. Логические схемы делителей на целое число обычно выполняются на так называемых JK-триггерах.
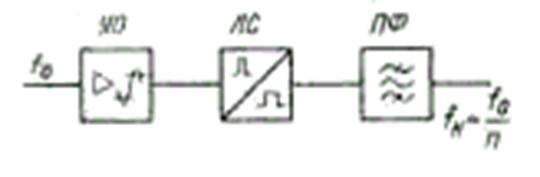 Рис. 6.65.
Структурная схема
Рис. 6.65.
Структурная схема
цифрового делителя.
Наиболее простой является ЛС для делителя на п
= 2°, где а - целое положительное число. Эта схема приведена на рис. 6.66, а.
На рис. 6.67 показаны ее временные диаграммы работы в точках а, 6, в
и г. Входная импульсная последовательность (точка а схемы)
показана на временной диаграмме а. Ее частота равна, а период Т0=1/2f0p. Будем считать, что в момент
включения триггер Тг1 находился в исходном состоянии, т. е. на его выходе
сигнал отсутствовал (точка б схемы). Тогда первый импульс, поступивший
на соединенные между собой входы триггера, заставит его опрокинуться, и на его
выходе Q появится сигнал/ Этот сигнал сохранится и после
того, как импульс на входе закончится, и пропадет только в результате
опрокидывания триггера при поступлении второго импульса входной последовательности
(график б). Таким образом, на выходе первого триггера имеет место
последовательность импульсов с периодом 2Т0. Следовательно, ячейка,
выполненная на одном триггере, является ЛС делителя частоты на п= 2![]() =2a =21=2.
=2a =21=2.
Если эту последовательность или обратную ей (график б) подать на объединенные входы следующего триггера Тг2, то на его выходе получим последовательность импульсов с периодом 4Т0, т. е. осуществим деление на п = 22 = 4 и т.д.
Часто для упрощения ЛС, состоящую из a каскадно включенных триггеров, изображают в виде одного триггера с указанием числа а (см. рис. 6.66, б).
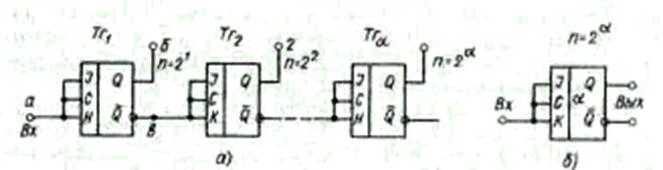
Рис. 6.66. Логическая схема делителя на 2a (а) и изображение
ее в виде одного триггера с указанием числа а (6)
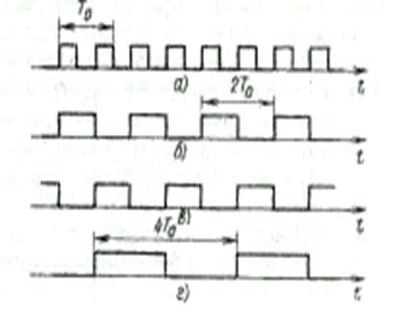
Рис.6.67. Временные диаграммы работы делителя 2a
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.