По выражениям для определения половины ширины разводья между льдинами различных форм и размеров можно проконтролировать результаты визуальной оценки сплоченности. С этой целью достаточно определить размер льдины ( средний на данном участке моря) и ширину разводья между двумя смежными льдинами. Затем по одной из предложенных выше формул уточнить фактическую сплоченность.
Модель распределения льда по C.K. Rheem.
C.K. Rheem, H. Yamaguchi и H. Kato предложили еще одну модель распределения масс льдин для вычисления реологических характеристик припайного льда. Когда моделируется движение припайного льда очень важно оценивать взаимодействие между отдельными льдинами, а также влияние очертания береговой линии или формы опоры сооружения.
Континуальные модели, предложенные для долговременных (1965,1992,1979 год) и краткосрочных предсказаний (1989,1988 год) имеют определенные ограничения, так как припайный лед имеет дискретные включения. С другой стороны (1993 год) была предложена модель дискретных элементов объединяющих каждую льдину в диск. Хотя этот подход и является интересным - практическое использование его затруднено из-за большого времени вычислений.
Модель распределенной массы дискретной льдины является новой моделью для численного моделирования реологии припайного льда. Она использует преимущества, как континуальной, так и дискретной модели. Эта модель выражает дискретный характер припайного льда, который является трудным для континуальной модели с точки зрения взаимодействия. Она может рассматривать взаимодействие большого количества льдин с более коротким временим вычислений по сравнению с моделью дискретного элемента.
Подобные модели с прямоугольными льдинами были описаны в прошлых работах (1993,1994 год). Эта статья описывает вариант модели ледяного диска.
Припайный лед делится на прямоугольные группы в которых льдины имеют равные размеры и допускаются распределенными однородными. Сила взаимодействия льда получается из соотношения между импульсом группы льдин и изменениями момента группы льдин. Модель может выражать боковое расширение припайного льда которое является трудным доля модели рассматривающей взаимодействие прямоугольной льдины. Уравнение движения группы получается из закона сохранения моментов взятых в соответствии с силой Кориолиса, силой наклона морской поверхности, силой взаимодействия между группами льдин, и давление возникает из-за ветра и течения воды.
Принята методика перемещения масс льда по Лагранжу: многослойная модель используется в моделировании течения морской воды одновременно с дрейфом льда для объяснения течения поверхности более точно.
Вычисления сделаны для различных упрощений океанских условий привязанных к однородному полю ветра в предельных (незначительных, крайних) ледовых зонах. Они предсказывают пространственное и временное распределение скорости льда, сил взаимодействия давлений и сплоченностей льда у береговой линии и вокруг сооружения.
Льдины моделируются как жесткие диски с равной площадью и толщиной в группе прямоугольной льдины. Допускают, что они распределены однородно. Группа льдин характеризуется значением их центра расположения S и сплоченностью льда Сi которая является соотношением общей площади льдины к площади группы:
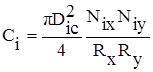 ,
(1.149)
,
(1.149)
где Rх и Rу - площадь группы льдин; pDic2/4 -площадь отдельной льдины; Niх и Niу - количество льдин в группе; Dic - диаметр льдины.
Уравнение движения группы.
Дрейф припайного льда с относительно коротким временным масштабом (порядка 7 дней) может быть численно хорошо смоделирован динамической моделью, где сила Кориолиса, сила наклона морской поверхности, сила взаимодействия между группами льдин, и давления возникающее из-за ветра и течения воды рассматривается пренебрегая ростом льда и таянием. Момент изменения группы льдин в интервал времени dt может быть выражена из уравнений:
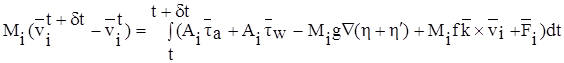 (1.150)
(1.150)
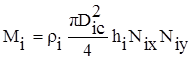 ,
(1.151)
,
(1.151)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.