Многоцикловое и истирающее воздействия дрейфующего ледяного покрова на морские гидротехнические сооружения (Описание ледового режима морских акваторий), страница 7

Этот метод основан на визуальной оценке сплоченности льда. Как известно, метод определения сплоченности льда N включает быструю оценку площади всех льдин Sл, площади участка моря Sм, на котором они равномерно распределены, и расчет их соотношений:

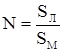,                                                              (1.141)

Вполне естественно, что точно определить площади всех льдин различных форм и горизонтальных размеров чрезвычайно сложно.

Следовательно, упрощение существующего метода наблюдений или разработка способа контроля визуальной оценки сплоченности льда, по-прежнему остается одной из актуальных задач. При решении ее наиболее перспективным, на наш взгляд, является путь поиска связи ширины промежутка чистой воды, разделяющей льдины, с размерами самих льдин при разной сплоченности льда.

Модель учета размеров льда по Ю.П. Доронину и Д.Е. Хейсину.

Аналитическое решение этой задачи было выполнено Ю.П. Дорониным и Д.Е. Хейсиным [ ]. Приняв ширину разводья (промежутка чистой воды между льдинами) 2Х и полагая, что между периметром и площадью льдин существуют определенные соотношения, они вывели следующую зависимость между половиной ширины разводья Х и сплоченностью:

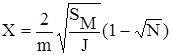,                                       (1.142)

где Х- половина ширины разводья, m- коэффициент пропорциональности, Sм - площадь участка моря, на котором распределены льды, J - количество льдин, N - сплоченность льда.

Для разряженных льдов Ю.П. Доронин и Д.Е. Хейсин вывели приближенную зависимость между сплоченностью льда и «длиной свободного побега» льдины (lс@2Х):

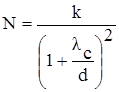,                                                  (1.143)

где к - коэффициент (немного меньше единицы), d - средний диаметр льдины.

Приведенные зависимости для сплоченных и разреженных льдов различаются. Их неудобно использовать для контроля оценки сплоченности льда, поскольку предварительно необходимо рассчитывать коэффициент пропорциональности m для каждой формы льдины, определить площадь участка моря, точно подсчитать количество льдин. Поэтому для определения ширины разводий при различной сплоченности льдов введем упрощенные выражения, учитывающие форму льдин и их горизонтальные размеры.

Пусть на участке моря АБВГ равномерно распределены льдины квадратной формы (рис.). Расстояние между льдинами (ширина разводья) составляет 2l, а сторона квадратной льдины а. Тогда Sл=4a², Sм=4(а+2l)², откуда

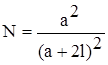,                                                     (1.144)

Решая это выражение относительно ширины разводья, получим

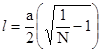,                                                      (1.145)

где l - половина ширины разводья.

При распределении льдин прямоугольной формы (рис. ) полуширина разводья l₁>l₂, поскольку а > b. Известно также, что a=kb [4,5], a l₁=kl₂. Из рис.  видно, что Sл=4ab, Sм=4(a+2l₁) (b+2l₂),откуда

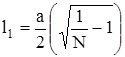
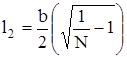                       (1.146)

При распределении на участке моря льдин круглой формы рассмотрим квадратическое (рис. ) и компактное (ромбическое) положение льдин (рис.  ).

При квадратическом расположении круглых льдин создаются дополнительные участки чистой воды в районах гиперболических точек О между каждыми четырьмя круглыми льдинами. Если не учитывать эти дополнительные площади чистой воды, то полуширина разводья составит

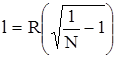,                                                   (1.147)

В направлении АА дополнительные участки чистой воды не будут оказывать влияния на сплоченность льда. Вместе с тем они изменят сплоченность льда в направлении РР. Расчеты показывают, что каждую круглую льдину или площадь, находящуюся в районе гиперболической точки О, приходится дополнительно участок воды, площадь которого равна

,                                              (1.148)

При компактном расположении льдин полуширина разводья без учета дополнительной площади чистой воды, возникающей в районе гиперболической точки О₁ или О₂, также определяется по формуле (1.148).