Точка их пересечения графиков изменения зависимостей (1.159) и (1.160) соответствует совместному решению этих уравнений.
Ледовая нагрузка в кинематической стадии нагружения представляется в виде:
,
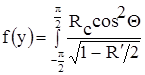
(1.161)
где Rс - из решения уравнений (24) и (25), зависящих от скоростей нагружения и дрейфа ледяных полей.
Уравнения колебаний конструкции опоры зависят от массы и жесткости ее различных частей.
Колебание верхней части конструкции описывается с помощью уравнений колебаний жесткого тела:
,
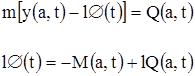(1.162)
Для нижних частей конструкции применяются уравнения поперечных колебаний балок под действием нагрузок q(х) с учетом сил демпфирования. Для расчета фундаментной части конструкции используется гипотеза коэффициента постели. Место сопряжения верхней жесткой части конструкции с нижней балочной частью может иметь податливость при относительном повороте.
Решение задачи о колебании всей системы конструкции в целом, ввиду нелинейности ледовой нагрузки ¦(y), может быть выполнено только численными методами. Для анализа общей устойчивости системы функция ¦(y) может быть линеаризирована путем разложения в ряд Маклорена. Устойчивость системы анализировалась с помощью построения Гамильтониана Н(t) как функционала Ляпунова. При Н(t)£0, система устойчива. Первое решение достигается всегда, для выполнения второго условия H(t)³0 необходимо, чтобы энергия возмущающих сил не превышала энергию демпфирования системы.
Модель Тояма и др. [ ]. Дальнейшее развитие динамический метод расчета взаимодействия льда и сооружения с позиций автоколебаний получил в работе [ ]. Теоретическая модель строилась на основе данных лабораторных исследований.
Использовались модели двух типов конструкций - моноподов (отдельно стоящие колонны, тип 1) и варианта двухколонной опорной части сооружения (тип 2) с расстоянием между центрами колонн 32 см. Диаметр колонн во всех случаях был равен 7.6 см.
Модели опор имели разную частоту собственных колебаний, которая имела следующие значения:
а) первый тип модели (монопод): 1-F, 1-A, 1-B, 1-E сооветственно wn = ¥; 16.0; 4.02; 1,27 Гц;
б) второй тип модели: 2-F, 2-F, 2-B, 2-E соответственно wn = ¥; 14.7; 4.01; 1.21 Гц.
Во всех случаях, за исключением начального этапа загружения, в опытах наблюдались периодические воздействия ледовой нагрузки и соответственно колебания моделей. В тоже время результаты экспериментов существенно зависели от частоты собственных колебаний моделей и скорости движения ледяного поля V. При малых скоростях перемещения ледяного поля (V=0.2-0.6 см/с) диаграммы загружения и перемещения моделей имеют пилообразный характер с периодом порядка несколько секунд. Для гибких конструкций моделей (E) характерно установившееся гармоническое колебание величины нагрузок и деформаций при больших скоростях движения ледяного поля.
Анализ экспериментов показал, что диапазон Du изменения разности максимальных значений перемещения моделей (тип 1, 2-E) Du минимального значения umin описываются эмпирической зависимостью:
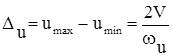, (1.163)
Зависимость (1.163) подтверждается автономностью установившегося колебательного процесса, что говорит о наличии негативного демпфирования в колебательной системе и возникновение процесса ее автоколебаний. Математическая модель этого процесса описывается авторами в виде уравнения:
,
(1.164)
где M, C, K - соответственно масса, коэффициенты демпфирования и жесткости; F(t) - ледовая нагрузка.
Упруговязкие деформации ледяного поля в расчет не принимаются. Предполагается, что нагрузка F(t) нарастает в пределах начальной фазы упругого деформирования конструкции до некоторого пикового значения F0 при U=V, U=0, затем резко падает до некоторой константы F0, называемой силой разрушения при дроблении. Дальнейший процесс колебания в пределах цикла разрушения рассматривается при F(t)=F0 и начальных условиях:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.